OpenGL ES和坐标变换（二） - 铁蕾的个人博客

首页 > 移动开发 > 正文

OpenGL ES和坐标变换（二）
2017-11-09

本文是《OpenGL ES和坐标变换》系列文章的第二篇。在本文中，我们将集中讨论以下内容：

首先，以Demo程序中的代码为例，介绍model、view、projection三个变换在Android中如何用代码来表达。
介绍相关理论，推导一下model变换中的缩放(scaling)和平移(translation)这两个变换的计算过程。由于旋转(rotation)这个话题比较复杂，我们留在下一篇再讨论。
我们分析一下Android中的缩放(scaling)和平移(translation)变换的具体实现，将前面的理论推导同代码实现相互印证，以加深理解。

著名数学家高斯曾经说过一句话：“当一幢建筑物完成时，应该把脚手架拆除干净。”他说这话的意思是，一个新的数学理论一旦推导完成，他就会把多余的东西（比如灵感来源、直观的想法、中间走过的弯路、多余的推导计算等等）统统删掉，只把最终得到的最简洁的定理和结论公布出来。高斯的理由是，「脚手架」会影响理论的美感。但是，没有这些所谓的「脚手架」，后人就很难理解他的理论。从学习的角度来说，这些「脚手架」却是大大的有用。试想，只是看到一座宏伟的大厦，你并不能学会如何去建造它。

本文为了让细节讨论更加清楚，当然不会按照高斯的这种风格。相反，在本文接下来的描述中，我们会尽量详尽地说明每一步推导过程，并尽可能把推导的思路说清楚。

Demo程序简介

上一篇已经给出了Demo程序的地址，为了明确，这里把地址再贴一遍。本文中出现的代码，都来自于下面这个文件：

https://github.com/tielei/OpenGLESTransformationsDemo/blob/master/app/src/main/java/com/zhangtielei/demos/opengles/transformations/MainActivity.java

首先，vertex shader中跟坐标变换有关的是下面这一行代码：

gl_Position = projection * view * model * vec4(position.xyz, 1);

它表示，对一个顶点坐标依次进行model、view、projection三种变换。这三种变换，分别是通过左乘一个矩阵来完成的。在上面这行代码中，看起来三个变换的顺序跟我们期望的相反了，但这正是矩阵左乘造成的结果。

代码中的vec4(position.xyz, 1)表示顶点在本地坐标系中的坐标（用一个四维的齐次坐标来表达，我们下面会介绍）。它左边乘上model矩阵，就得到了该顶点在世界坐标系中的坐标。上一篇我们已经讲过，这个model变换可能包含了缩放(scaling)、旋转(rotation)、平移(translation)这三种变换。然后，世界坐标系中的坐标再左乘一个view矩阵，就变换到了相机坐标系。最后，再左乘projection矩阵，就完成了投影变换。

那么这行代码中的model、view、projection这三个矩阵，它们的值是什么呢？我们看一下在Demo程序中它们的值是怎样分别计算的。以第2个立方体为例，计算model矩阵的代码如下：

Matrix.setIdentityM(modelMatrix2, 0);
Matrix.translateM(modelMatrix2, 0, 0.5f, 1.0f, -1.5f);
Matrix.rotateM(modelMatrix2, 0, angle, 0.0f, 1.0f, 0.0f);
Matrix.scaleM(modelMatrix2, 0, 1.5f, 1.5f, 1.5f);

这段代码中的modelMatrix2就是要计算的model矩阵，它是一个4x4的矩阵，存储在一个长度为16的float数组里(float[16])。为什么不是3x3的矩阵呢？这跟齐次坐标有关，我们后面再说，现在先不管它。我们调用了Android SDK中的Matrix工具类的方法对其进行了赋值。setIdentityM表示设置一个初始的单位矩阵，而translateM, rotateM和scaleM表示在这个初始的单位矩阵基础上依次对矩阵进行调整，即依次进行平移、旋转、缩放的调整操作。需要注意的是，这里的代码调用顺序虽然是先平移，然后旋转，最后再进行缩放，但这些操作的含义却需要反过来解释，也就是说先进行了一个缩放操作，然后进行了旋转，最后才执行了平移操作。这其中的原因仍然与矩阵左乘的含义有关，相关细节我们会在本文最后一部分再详细解释。现在我们暂且记住这些操作的解释顺序，那么上面这段代码的精确含义就是：

缩放：先在x, y, z三个坐标轴上都放大1.5倍；
旋转：再绕着向量[0.0, 1.0, 0.0]^T(也就是y轴)旋转角度angle；
平移：沿x轴正向平移0.5个单位，沿y轴正向平移1.0个单位，沿z轴负向平移1.5个单位。

如果你已经运行了Demo程序，那么根据上面这段描述，你就会看到这个立方体正是屏幕最上面的那个最大的立方体。它沿着一个轴在不停地旋转。之所以会旋转，是因为上面第2步中旋转的角度angle是个动态的值，它的值每一帧都在变化，所以看起来在不停地旋转。

看到这里，估计有些同学禁不住会想，在上面的描述中，y轴是不是就是指向屏幕的上方？z轴是不是就是垂直于屏幕？不是的。当我们提到坐标以及坐标轴的时候，我们首先必须搞清我们当前在谈论的到底是哪个坐标系。在整个计算过程中，我们经常会在不同的坐标系之间切换。根据上一篇的介绍，我们当前正在谈论的model变换是从本地坐标系变换到世界坐标系，因此，这里的x, y, z三个坐标轴指的是世界坐标系。而世界坐标系与屏幕的角度和位置没有直接关系，这取决于后面的view变换（从哪个角度去观察）。

接下来，我们再看一下在Demo程序中view矩阵是怎样计算的。

Matrix.setLookAtM(viewMatrix, 0, 3.0f, 3.0f, 10.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f);

这行代码中的viewMatrix就是要计算的view矩阵，它也是一个4x4的矩阵。我们仍然是调用了Matrix工具类的方法对其进行了赋值。它表达的意思是：我们把眼睛（或者说相机）放在世界坐标系的(3.0, 3.0, 10.0)这个点，然后观察的方向正对着点(0.0, 0.0, 0.0)，即世界坐标系的原点。同时我们还需要指定一个「头朝上」的方向，这在代码里设置的是向量(0.0, 1.0, 0.0)指向「上」的方向。

最后看一下projection矩阵的计算：

Matrix.perspectiveM(projectionMatrix, 0, 45.0f, width / (float) height, 0.1f, 100.0f);

这行代码中的projectionMatrix就是要计算的projection矩阵，它同样也是一个4x4的矩阵。Matrix.perspectiveM对这个矩阵进行了赋值，这个调用需要的几个输入参数如下：

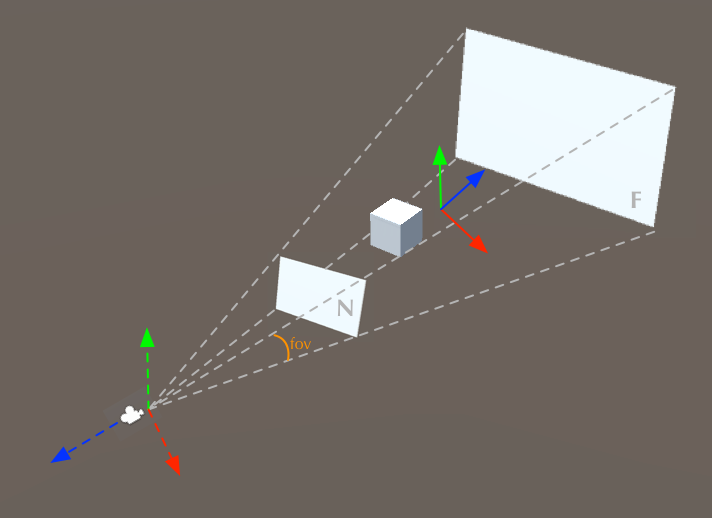
观察视角为45.0度。这个值通常被称为field of view，简称fov。它的含义已在下图中标出。

第二个参数为宽高比，指的是近平面(N)的宽高比。
第三和第四个参数分别表示近平面(N)和远平面(F)与相机的距离。

现在，与model、view、projection三个矩阵的计算有关的代码我们都看到了，已经粗略知道了整个计算的流程。下一节我们就定量地分析一下其中某些矩阵的计算过程。

缩放和平移矩阵的推导

关于线性代数理论基础的说明

在前面（包括上一篇）我们提到坐标变换的时候，一直在说对顶点进行变换，但是，我们知道，在线性代数中我们研究的概念都是基于向量的，并没有点的概念。向量的原始概念是一个由n个数组成的n元数组。当把向量对应到几何空间中的时候，我们才有了点的概念，以及点和向量的关系。

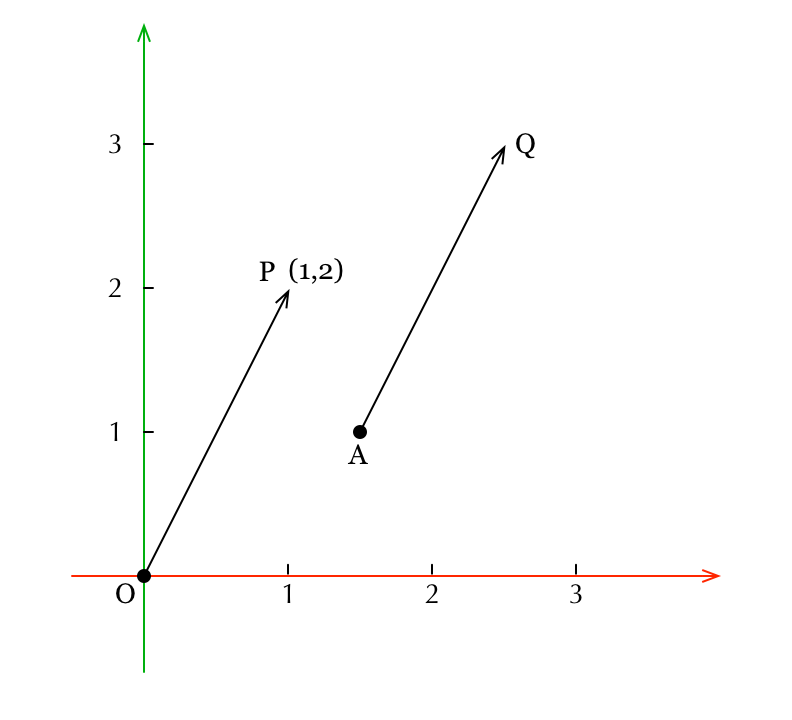
如上图，我们建立了一个直角坐标系， $\boldsymbol{\overrightarrow{OP}}$ 就是一个向量，它表示一个有大小和方向的量。把它表示在坐标系里的时候，起点在原点O，终点指向点P。这个向量的坐标和点P的坐标一样，都可以记为(1,2)。也就是说，任意一个点和一个由原点指向该点的向量是可以一一对应的，这样我们这里讲的OpenGL ES里对于顶点(vertex)的坐标变换，就可以和线性代数里讲的对于向量的线性变换以及坐标变换的知识，对应起来了。

在后面的描述中，为了方便，我们有时候会说对向量进行变换，有时候会说对点(或顶点)进行变换，这两种说法是等价的，因为一个点和一个起点在原点且终点在这个点的向量一一对应。

在直角坐标系中表达的向量还有一个性质，就是向量与起点位置无关，也就是说，一个向量向任意方向平移之后不变。比如，在上图中， $\boldsymbol{\overrightarrow{AQ}}$ 是由向量 $\boldsymbol{\overrightarrow{OP}}$ 平移之后得到的向量，平移前后它们的大小和方向都一样，所以它们表示相同的向量。所以，平移后的向量 $\boldsymbol{\overrightarrow{AQ}}$ 仍然以坐标(1,2)来表达。

既然向量平移后坐标不变，那么我们要对顶点进行平移变换，就不能直接通过对一个向量的平移来得到。实际上，我们会用到两个向量的加法（下一节我们马上会看到）。

在线性代数中，我们有线性变换的概念，它的理论基础非常丰富和完善，但是我们要讨论的OpenGL ES里的各个变换过程，却不能完全被线性变换所囊括。比如，缩放和旋转可以用线性变换来表达，但平移不能。我们后面要讨论的view变换和投影变换，也不属于线性变换。实际上，它们属于仿射变换(Affine Transformation)的范畴。我们先不过早地进入这些抽象概念的讨论，而是对于每个变换具体地去讨论它们的推导过程。也许到最后，当我们回过头来再看这些抽象概念的时候，会看得更加清楚。

平移矩阵的推导过程

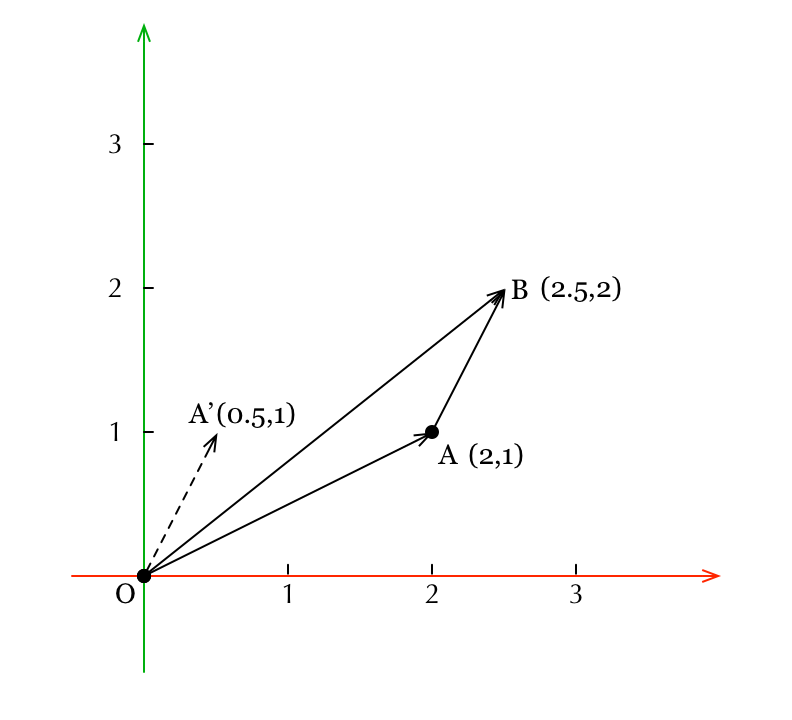
首先，我们先来考虑顶点的平移(translation)。这可以通过向量加法来完成。见下图。

图中A点平移到B点，相当于做一个向量加法：

$\boldsymbol{\overrightarrow{OA}} + \boldsymbol{\overrightarrow{AB}} = \boldsymbol{\overrightarrow{OB}}$

我们看到，在直角坐标系中，向量加法满足三角形法则。其中向量 $\boldsymbol{\overrightarrow{AB}}$ 代表了平移的大小和方向，称为平移向量(translation vector)。为了更清楚地读出这个平移向量的坐标，我们把它平移到原点处，它和向量 $\boldsymbol{\overrightarrow{OA'}}$ 相等，能看出它的坐标是(0.5,1)。向量 $\boldsymbol{\overrightarrow{OA}}$ 加上这样的一个平移向量，相当于把点A沿x轴平移0.5个单位，并沿y轴平移1个单位，这样就平移到了点B的位置。

前面图中是2维向量的例子，现在我们扩展到3维，将平移变换用向量坐标来表示，如下：

$\begin{bmatrix} x \\ y \\ z \end{bmatrix} + \begin{bmatrix} T_x \\ T_y \\ T_z \end{bmatrix} = \begin{bmatrix} x + T_x \\ y + T_y \\ z + T_z \end{bmatrix}$

上式中的

$\begin{bmatrix} T_x \\ T_y \\ T_z \end{bmatrix}$

就代表前面提到的平移向量(translation vector)的值。

在线性代数中，一个变换通常使用矩阵的乘法来表达。况且OpenGL ES使用GPU来进行运算，而GPU对于矩阵乘法有着非常高效的算法。我们也希望这里的平移变换能用矩阵乘法（具体说是左乘）来表达。我们设想一个3x3的矩阵A，让它乘上顶点的3维坐标：

$\boldsymbol{A} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} a_{11}x + a_{12}y + a_{13}z \\ a_{21}x + a_{22}y + a_{23}z \\ a_{31}x + a_{32}y + a_{33}z \\ \end{bmatrix}$

我们发现，无论矩阵A的各个元素取什么样的值，我们只能得到x,y,z的线性组合，而怎么样也得不到类似前面向量加法的结果形式（x,y,z分别加上一个常数）。为了解决这个问题，我们将3维的顶点坐标换成4维的齐次坐标(homogeneous coordinates)。所谓齐次坐标，就是在3维坐标的基础上，加上第4个维度，并把它的值设成1。也就是说，3维坐标

$\begin{bmatrix} x \\ y \\ z \end{bmatrix}$

变成齐次坐标就是：

$\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}$

当然，齐次坐标的第4个元素，也可以不是1，不过这种情况我们暂时用不到，等我们讨论到投影变换和perspective division的时候再仔细探讨这种情况。现在我们暂且简单的认为，齐次坐标就是多了第4个维度，并且它是一个固定的1。可以想象，多出来的这个1对我们至少没有什么坏的影响，只要在需要的时候把它去掉，我们就能得到原来的3维坐标。实际上，在OpenGL ES中，我们总是以4维的齐次坐标来表示顶点坐标。回想一下前面vertex shader程序中的vec4(position.xyz, 1)，就是一个齐次坐标。

这样，一个4维的顶点坐标经过左乘一个矩阵，得到的结果也是一个4维的顶点坐标（仍然是个齐次坐标）。这个矩阵需要是4X4的。根据矩阵乘法的定义，现在我们很容易拼出一个能表示平移的矩阵来：

$\begin{bmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x + T_x \\ y + T_y \\ z + T_z \\ 1 \end{bmatrix}$

上式中的矩阵：

$\begin{bmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

正是我们要推导的平移矩阵。它是4x4的。我们发现，它左上角是一个3x3的单位矩阵，第4列前3个元素恰好是平移向量。可以看出，正是由于我们使用了齐次坐标的表达形式，多了一个第4维度的1，才使得上面经过矩阵乘法之后得到了向量加法的结果形式（x,y,z加上平移向量）。

缩放矩阵的推导过程

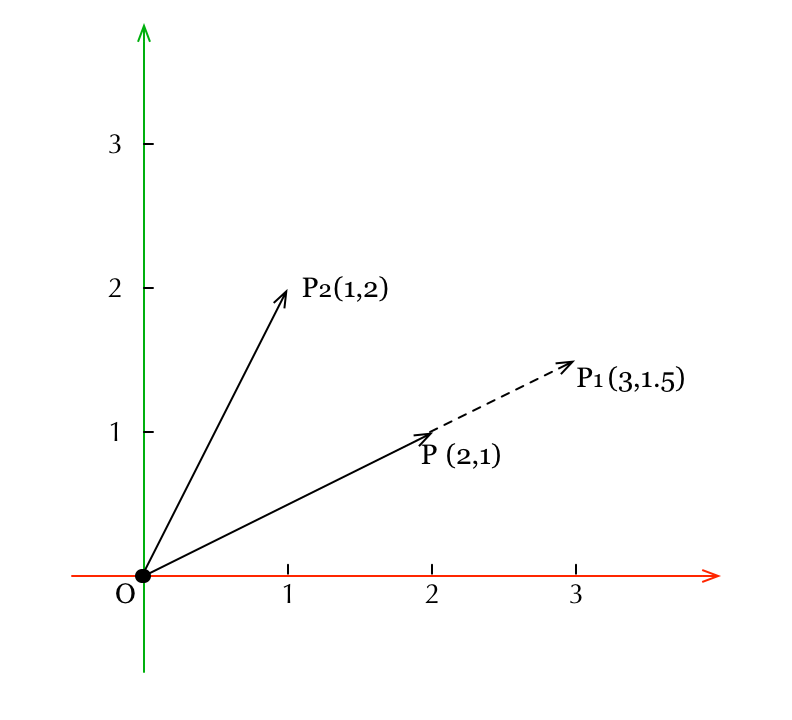
上图表达了2维向量的缩放过程。向量 $\boldsymbol{\overrightarrow{OP}}$ 在x和y方向上都放大了1.5倍就得到了向量 $\boldsymbol{\overrightarrow{OP_1}}$ ，坐标从(2,1)变换成了(3,1.5)。这种缩放方式比较符合我们常识中的「放大」或「缩小」，即各个维度上都「放大」或「缩小」相同的倍数。如果在3D空间中的一个对象的各个顶点都「放大」或「缩小」相同的倍数，那么这个3D对象本身就「放大」或「缩小」了相应的倍数。

但是，OpenGL ES里的缩放变换可以表达更一般的情形，也就是各个维度上缩放不同的倍数。还是以上图2维向量为例，向量 $\boldsymbol{\overrightarrow{OP}}$ 在x方向上缩小为原来的0.5倍，在y方向上放大为原来的2倍，就得到了向量 $\boldsymbol{\overrightarrow{OP_2}}$ ，坐标从(2,1)变换成了(1,2)，这也是一种缩放变换。

从上面的例子可见，缩放变换就是把各个维度的坐标分别「放大」或「缩小」一个倍数。扩展到3D空间，仍然使用4维的齐次坐标，缩放操作用矩阵乘法可以写成：

$\begin{bmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} S_xx \\ S_yy \\ S_zz \\ 1 \end{bmatrix}$

上面这个式子意思就是，一个向量的x,y,z坐标经过缩放变换之后，分别变成了原来S_x,S_y,S_z倍。而式子中左乘的这个4x4的矩阵，就是我们要推导的缩放矩阵：

$\begin{bmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

Android中缩放和平移的实现

最后我们看一下，前一节推导出来的平移矩阵和缩放矩阵在Android中是怎样计算出来的。在Android中，有一个工具类，名字叫android.opengl.Matrix（请注意包名），用来计算常见的变换矩阵。

按说我们前面已经推导出了平移矩阵和缩放矩阵的表达式，它们都表达为4x4的矩阵，而且形式也不复杂，那么如何用代码实现出来似乎也是显而易见的。然而，如果把本文第一节出现的代码与推导得到的矩阵表达式进行仔细对比，就会发现事情还没那么简单。

从理论上讲，顶点的变换过程可以表示为：一个4维的顶点齐次坐标，左乘上一个4x4的变换矩阵，就得到了变换后的顶点齐次坐标。如果一个顶点坐标要进行多个变换，比如，先进行缩放变换，再进行平移变换，那么应该先左乘缩放矩阵，再左乘平移矩阵。但是，我们在第一节中介绍的代码中，是在一个初始的单位矩阵基础上依次对矩阵进行调整，也就是依次进行平移、旋转、缩放的调整操作（即分别调用了Matrix的translateM, rotateM, scaleM三个工具方法）。这段代码我们再贴一遍，如下：

Matrix.setIdentityM(modelMatrix2, 0);
Matrix.translateM(modelMatrix2, 0, 0.5f, 1.0f, -1.5f);
Matrix.rotateM(modelMatrix2, 0, angle, 0.0f, 1.0f, 0.0f);
Matrix.scaleM(modelMatrix2, 0, 1.5f, 1.5f, 1.5f);

最终得到的矩阵modelMatrix2传到vertex shader中去，相当于在顶点坐标上先左乘缩放矩阵，再左乘旋转矩阵，然后再左乘平移矩阵，跟代码调用的顺序正好相反。这到底是怎么回事呢？

我们先单独观察Matrix.scaleM这一步调用，分析一下。这个方法的签名是这样的：

public static void scaleM(float[] m, int mOffset,
            float x, float y, float z);

它表达的意思是，输入的float数组m在偏移mOffset处已经存放着一个变换矩阵了(是4x4的)，记这个矩阵为M。经过scaleM这个调用之后，输入的这个变换矩阵在原地进行一定的调整，加入了缩放操作，形成了一个新的变换矩阵，记为M’。最终得到的这个新矩阵M’左乘到顶点坐标上去，得到的最终效果就是先把顶点坐标的三个维度分别缩放到原来的x,y,z倍，然后再执行原来的变换M。注意：这里x,y,z这三个参数，相当于前面推导过程中的S_x,S_y,S_z。

记前面推导出来的缩放矩阵为S，即：

$\boldsymbol{S}= \begin{bmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

那么，必然有：

M’ = M S

只有这样，当把M’左乘到某顶点坐标上去的时候，才能解释成：先缩放，然后再执行变换M。

注意：这个公式表达的意思可以概括为，经过scaleM处理，相当于在原来的变换矩阵的基础上右乘了一个缩放矩阵。

为了看清楚这一步「右乘」到底做了什么操作，我们设任意的变换矩阵M为：

$\boldsymbol{M}= \begin{bmatrix} m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34} \\ m_{41} & m_{42} & m_{43} & m_{44} \\ \end{bmatrix}$

右乘上S之后，得到：

$\boldsymbol{M'}= \begin{bmatrix} m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34} \\ m_{41} & m_{42} & m_{43} & m_{44} \\ \end{bmatrix} \begin{bmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} m_{11}S_x & m_{12}S_y & m_{13}S_z & m_{14} \\ m_{21}S_x & m_{22}S_y & m_{23}S_z & m_{24} \\ m_{31}S_x & m_{32}S_y & m_{33}S_z & m_{34} \\ m_{41}S_x & m_{42}S_y & m_{43}S_z & m_{44} \\ \end{bmatrix}$

上面这个式子就表达了scaleM应该执行的操作：对原变换矩阵M的前三列各个元素分别乘以S_x,S_y,S_z；第4列保持不变。

现在我们来看一下scaleM的实现代码：

    public static void scaleM(float[] m, int mOffset,
            float x, float y, float z) {
        for (int i=0 ; i<4 ; i++) {
            int mi = mOffset + i;
            m[     mi] *= x;
            m[ 4 + mi] *= y;
            m[ 8 + mi] *= z;
        }
    }

这段代码恰恰就是前面的式子所表达的。这里需要注意的一点是：android.opengl.Matrix中的矩阵都是按照列顺序(column-major order)来存放的，所以代码中的m矩阵，它的每一列实际存放了矩阵的每一行。具体来说，它的数据存放顺序是这样的：

  m[offset +  0] m[offset +  4] m[offset +  8] m[offset + 12]
  m[offset +  1] m[offset +  5] m[offset +  9] m[offset + 13]
  m[offset +  2] m[offset +  6] m[offset + 10] m[offset + 14]
  m[offset +  3] m[offset +  7] m[offset + 11] m[offset + 15]

这样前面这段scaleM的代码实现就容易看懂了。

利用同样的思路，我们也可以推导出Matrix.translateM的计算过程。它相当于在任意的变换矩阵M上右乘平移矩阵T，得到一个新的变换矩阵M’。

根据上一节的理论推导，我们知道平移矩阵的值为：

$\boldsymbol{T}= \begin{bmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

计算M’为：

$\boldsymbol{M'}= \begin{bmatrix} m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34} \\ m_{41} & m_{42} & m_{43} & m_{44} \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} m_{11} & m_{12} & m_{13} & m_{11}T_x + m_{12}T_y + m_{13}T_z + m_{14} \\ m_{21} & m_{22} & m_{23} & m_{21}T_x + m_{22}T_y + m_{23}T_z + m_{24} \\ m_{31} & m_{32} & m_{33} & m_{31}T_x + m_{32}T_y + m_{33}T_z + m_{34} \\ m_{41} & m_{42} & m_{43} & m_{41}T_x + m_{42}T_y + m_{43}T_z + m_{44} \\ \end{bmatrix}$

这个式子就表达了translateM应该执行的操作。可以看出，原变换矩阵M的前三列不动，变化的只有第4列。

我们来看一下translateM的实现代码，它正是实现了前面这个式子的计算：

    public static void translateM(
            float[] m, int mOffset,
            float x, float y, float z) {
        for (int i=0 ; i<4 ; i++) {
            int mi = mOffset + i;
            m[12 + mi] += m[mi] * x + m[4 + mi] * y + m[8 + mi] * z;
        }
    }

由于本文尚没有深入讨论旋转变换，所以Matrix.rotateM这里就不讨论了，我们留在下一篇。

总结一下，本文重点讨论了model变换中平移矩阵和缩放矩阵的计算以及代码实现过程，虽然还没有详细介绍顶点坐标变换的其余部分，但已经基本说明了这整个的分析思路。这个系列后面的文章仍然会遵循这一思路，等不及的读者应该已经可以按照类似的方法开始自己的探索之旅了。

下一篇我们将讨论坐标变换中一个非常重要的变换——旋转。

（完）

其它精选文章：

原创文章，转载请注明出处，并包含下面的二维码！否则拒绝转载！
本文链接：http://zhangtielei.com/posts/blog-opengl-transformations-2.html
欢迎关注我的个人微博：微博上搜索我的名字「张铁蕾」。

上篇：为什么有些技术书籍难以读懂？

下篇：天赋是个伪命题吗？

OpenGL ES和坐标变换（二）
2017-11-09

Demo程序简介

缩放和平移矩阵的推导

关于线性代数理论基础的说明

平移矩阵的推导过程

缩放矩阵的推导过程

Android中缩放和平移的实现

栏目分类

最新文章

OpenGL ES和坐标变换（二） 2017-11-09

Demo程序简介

缩放和平移矩阵的推导

关于线性代数理论基础的说明

平移矩阵的推导过程

缩放矩阵的推导过程

Android中缩放和平移的实现

栏目分类

最新文章

OpenGL ES和坐标变换（二）
2017-11-09