首页 > AI技术 > 正文

科普一下：拆解LLM背后的概率学原理

2024-11-01

---

当我开车载着全家人做长途旅行时，为了打发时间，我们有时候会玩起「成语接龙」的游戏，类似这样：

海阔天空
空前绝后
后发制人
人山人海
…

游戏的规则是，每个人轮流说出一个成语。

当某个成员一时想不出来的时候，其他人通常会帮助他/她想出来一个合适的成语，使得接龙游戏能够继续下去。一般情况下，过不了太长时间，成语就会开始重复。比如，就像上面给出的例子，「人山人海」的下一个成语很可能又是：「海阔天空」！

条件概率和预测下一个token

当我们在说话或写文字的时候，其实也可以看成是在进行某种类似的「接龙游戏」，只不过这个过程更加微妙，涉及到的语言规模也更加庞大。

在成语接龙游戏中，我们根据前一个成语来「预测」下一个成语。而在说话或写作时，我们不停地在「预测」下一个字或下一个词语。虽然像成语接龙那么强的语境规则不再存在了，但是，我们需要随时在更大的语言空间内搜索词句，让语句或文段变得自然，并符合最基本的语法和常识。

相信很多人都有过这样的体验：当进行远程通话时，即使信号断断续续，你可能仍然能够大致听懂对方要表达的意思。这是因为，你的大脑根据已经掌握的语言知识以及常识，及时地「预测」出了对方词句中缺失的部分。

在自然语言处理 (NLP) 中，我们通常用一个条件概率来描述这一预测过程的概率分布。

假设我们已经知道了一段文本的前面n-1个字：w₁w₂…w_n-1，那么第n个字w_n出现的概率是：

P(w_n|w₁w₂…w_n-1)

现在的LLM，通过在大规模的文本语料上进行训练，就是学会了这样的一个条件概率（至于如何学会的，后面章节再讨论）。当然，LLM通常进行预测的单元不直接是字或词，而是token。这就是所谓的predict next token。

在本文中，我不打算涉及token和字词的区别这样的细节。读者可以姑且认为一个token就是一个字或一个词语（这不影响理解）。但是，在后面的章节中，我们将换用token的概念来进行描述。也就是说，从w₁到w_n，每一个变量都代表一个token。

前面的式子P(w_n|w₁w₂…w_n-1)，则表示，在知道了前n-1个token的前提下，预测第n个token的条件概率。

联合概率分布与生成式模型

假设某个LLM已经学会了如何预测前面的条件概率，那么，w_n需要在整个字典中进行取值。也就是说，对于字典中的任何一个可能的token，LLM都能预测出它在序列中第n个位置出现的概率。在机器学习中，这是一个分类问题，只是我们面临的类别数目非常庞大。以汉语为例，汉字的总量大约在十万量级左右（token字典的规模也应该在同一个数量级）。

我们知道，在机器学习中，解决分类问题有三种方法[1]，复杂度从高到低分别是：

• Generative Model：生成式模型。直接预测整个联合概率分布P(x,C_k)。
• Discriminative Model：判别式模型。只预测后验的条件概率分布P(C_k|x)。
• Discriminant Function：判别函数。直接将输入x映射到类别C_k，不涉及到概率分布。

对应到LLM，它对于生成序列的预测上，我们会发现：

• 联合概率分布，相当于计算P(w₁w₂…w_n-1w_n)。
• 条件概率分布，相当于计算P(w_n|w₁w₂…w_n-1)。

在上一小节，我们已经给出了条件概率的公式，LLM可以用它来predict next token。那么，这难道说明，LLM属于判别式模型？

等一下，似乎不太对！最常见的LLM，基本都是基于GPT架构的。大家都知道，GPT的全称是Generative Pre-trained Transformer，这里面的Generative一词，清楚地表明了它属于生成式模型。

这是怎么回事呢？对于序列的建模，有它的特殊性。当我们说，模型可以预测条件概率P(w_n|w₁w₂…w_n-1)的时候，我们的意思是说，这个预测对于任意的n都成立！也就是说，以下的条件概率，LLM都能够预测出来：

• P(w₂|w₁)
• P(w₃|w₁w₂)
• P(w₄|w₁w₂w₃)
• …
• P(w_n|w₁w₂…w_n-1)

我们发现，根据概率论的链式法则，把上面这些条件概率全部乘起来，再在前面乘以一个P(w₁)，就会得到：

P(w₁) P(w₂|w₁) P(w₃|w₁w₂) … P(w_n|w₁w₂…w_n-1) = P(w₁w₂…w_n-1w_n)

可见，LLM是能够预测一个序列的联合概率分布的（只不过需要多步来完成，每步只预测一个token）。严格来说，上面的等式左面还多了一个P(w₁)，但由于实际中LLM在生成时总会输入一个长度大于0的前缀序列，所以多出来的这一项P(w₁)不影响大局。

因此，我们可以说，LLM是货真价实的生成式模型。而上一小节的条件概率和本小节的联合概率分布，在描述LLM的能力时是等价的。

根据机器学习的一些理论基础，我们知道，生成式模型的主要优劣势如下：

• 优势：由于生成式模型学到了联合概率分布，因此它可以方便地生成新的数据样本。这使它适合解决创作类的生成任务。
• 劣势：对于算力和训练数据的规模，要求极大。

这些情况，与LLM的实际情况吻合。

离散和连续

在本文第一小节，为了做到predict next token，我们已经定义了条件概率P(w_n|w₁w₂…w_n-1)。现在，我们来讨论一下，这个条件概率如何才能够计算出来。

一个自然的想法可能是，通过统计计数的方法来估算。假设有一个很大的文本语料库，我们可以统计出这个语料库中序列w₁w₂…w_n-1出现的次数，记为C(w₁w₂…w_n-1)。容易想象出，在这个语料库中，序列w₁w₂…w_n-1的下一个token，可能是w_n，也可能不是。我们再计算出序列w₁w₂…w_n-1w_n在语料库中出现的次数，记为C(w₁w₂…w_n-1w_n)。于是，前面的条件概率可以用这两个次数的比值来估算：

P(w_n|w₁w₂…w_n-1) ≈ C(w₁w₂…w_n-1w_n) / C(w₁w₂…w_n-1)

这种估算条件概率的方法，其实就是早期的n-gram语言模型所使用的方法。它的计算有一定的道理，但却存在一个致命的问题：对于语料库中不存在的序列，以上公式中的两个次数都无法计算出来。由于语言是具有创造性的，所以即使语料库再大，也不可能涵盖所有可能出现的token序列。在真实的语言任务中（比如写作），通常不太可能像本文开头的成语接龙那样，那么容易就会出现重复。

这里面临一个很重要的generalization的问题：如何从训练语料库中已经见过的序列，估算出从未出现过的新序列的概率分布。

对于语言的建模是个离散的问题。我们前面提到过，语言的字典规模可能在十万量级，规模很大。但token不能取任意实数，它只能在字典中取值，因此是离散的。离散系统有一个问题：即使输入序列产生非常微小的变化（变成了新的序列），对这个新序列的概率的预估，也可能变化非常剧烈。这显然不是所期望的。

为了解决这个致命的问题，对语言序列进行的建模，我们必须选择具备连续性的概率模型。我们知道，神经网络是基本具备这样的特性的。

图灵奖得主Yoshua Bengio和他的同事在2003年的一篇文章[2]，比较好地解决了这一问题：

• 将离散的token表达成连续的embedding（原文中称为word feature vector）。这使得语义上相似的token，在embedding空间中也具备近似的数值。
• 使用具备连续性的神经网络来表达概率模型（也就是前面的联合概率分布）。

以此为基础，后面学术界又出现了很多对自然语言建模的重要进展，特别是2017年出现的Transformer[3]。后来的GPT-2[4]，GPT-3[5]，也都是在这些研究的基础上发展出来的。

概率的随机性和函数的确定性

我们前面一直在谈论概率分布，然后又提到了使用神经网络来表达这个概率分布。但这里似乎存在一个让人困惑的问题：概率在本质上是随机的，而神经网络本质上却是个确定性的函数，这两者是怎样调和到一起的？

本来这算不上一个问题，只是理解和认知上的。但我跟一些参加面试的候选人聊的时候发现，即使是统计学或机器学习专业的同学，似乎对这个问题也很困惑。因此，我们在这里展开讨论一下这个问题（虽然有些费口舌）。

如前所述，我们想要建模的，是一个概率，也就是：P(w_n|w₁w₂…w_n-1)。它表示，在知道了前n-1个token的前提下，预测第n个token的条件概率。也就是说，即使我们知道了前n-1个token作为输入序列，第n个token到底是什么，也没办法百分之百确定。这就是一个概率的意思。

但是，神经网络本质上是一个函数。你输入一个x，它就确定性地输出一个y。当然了，LLM也是一个神经网络，一个复杂一些的神经网络。

那么，一个本质上用来表达随机性的概率分布，为什么可以用一个确定性的函数来描述呢？答案存在于概率学本身。

首先，在概率论中，任何一个随机变量的概率分布，都是表达成一个函数的。随机变量有两种：离散随机变量和连续随机变量。

• 离散随机变量使用概率质量函数 (Probability Mass Function) 来表达，简称为PMF。通常用函数P(x)来表示。
• 连续随机变量使用概率密度函数 (Probability Density Function) 来表达，简称为PDF。通常用函数p(x)来表示。

不管是P(x)还是p(x)，它们都是随机变量x的函数。我们前面说过，LLM是一个离散的概率模型。因此下面我们重点关注P(x)。

虽然P(x)是x的函数，这里确实出现了函数，但是，在实际的机器学习问题中，一般来说，我们的目标是去预测x取某个特定值的时候的概率。这时候P(x)就变成一个常量了。我们发现，自变量x消失了。

真正让机器学习模型以一个复杂的函数（比如神经网络）的形式来呈现的原因，主要是两个：

• 很多机器学习问题，都是预测条件概率。如前所述，LLM也是如此。条件概率可以写成P(y|x)，它应该是关于x和y的函数。但我们的目标一般是去预测y取某个特定值的时候的条件概率，所以模型只需要表达成关于x的函数。
• 随机变量的函数，也是一个随机变量，它的概率分布也是原始随机变量的函数。假设z=g(x)，那么z也是一个随机变量，且它的概率分布P(z)是关于z的函数。而z是关于x的函数，所以P(z)也是关于x的函数。

显然，这两个原因，是存在于概率学本身的。

现实中的实际问题一般都是比较复杂的，对这些问题进行建模，也需要足够复杂的函数来描述一个概率分布。对神经网络来说，输入x一般指的是条件概率中表示给定事件的那个随机变量，它每经过网络的一层，就经过一次函数变换（而且是非线性的）。可以想象，经过足够多层的变换，最终得到的函数应该是个足够复杂的函数。实际上，神经网络是可以近似任何函数计算的[6]。

简单总结一下：概率是用来表达随机性的，但在数学上是用一个确定性的函数来描述的。神经网络经过多层的函数变换，最终能够近似表达任意的函数，也就能够近似表达任意的概率分布。

最后，回到LLM生成模型，它和其他神经网络一样，经过一系列函数计算，得到了条件概率P(w_n|w₁w₂…w_n-1)的确定值。然后，还要经过一个采样（Sampling）的过程，才能真正得到要生成的token。前面的函数计算是确定性的过程；后面的采样则是表现了随机性的过程，而且随机性的程度大小可以使用温度值 (temperature) 来控制（温度值的细节本文不展开）。

预训练和指令微调

至此，我们还遗留了一个问题：LLM是怎么学会语言的联合概率分布的？

先回顾一下我几年之前写的一篇文章《深度学习、信息论与统计学》中所提到的：模型训练时使用的loss function，通常来源于最大似然估计 (Maximum Likelihood Estimation)，简称为MLE。

在预训练阶段，对于LLM生成模型来说，MLE意味着让模型不断调整参数，使得从模型中采样得到的（即生成的）序列恰好等于整个训练集（即训练语料库）的概率达到最大。同样在这篇文章中，我们还推导了另一种等价形式，训练过程也可以看成是使得训练集分布p’_data与模型分布p_model之间的Cross-Entropy最小化的过程。这个Cross-Entropy的值记为：

H(p’_data, p_model) = -E_x~p’data[log p_model(y|x;θ)]

根据本文第一小节，这个式子中的x和y分别应该对应：

• x = w₁w₂…w_n-1
• y = w₂w₃…w_n

这其实就是Transformer中广泛使用的自回归方法 (auto-regressive) ，predict next token。注意，在训练时，理论上w₁w₂…w_n-1w_n应该遍历整个训练集。

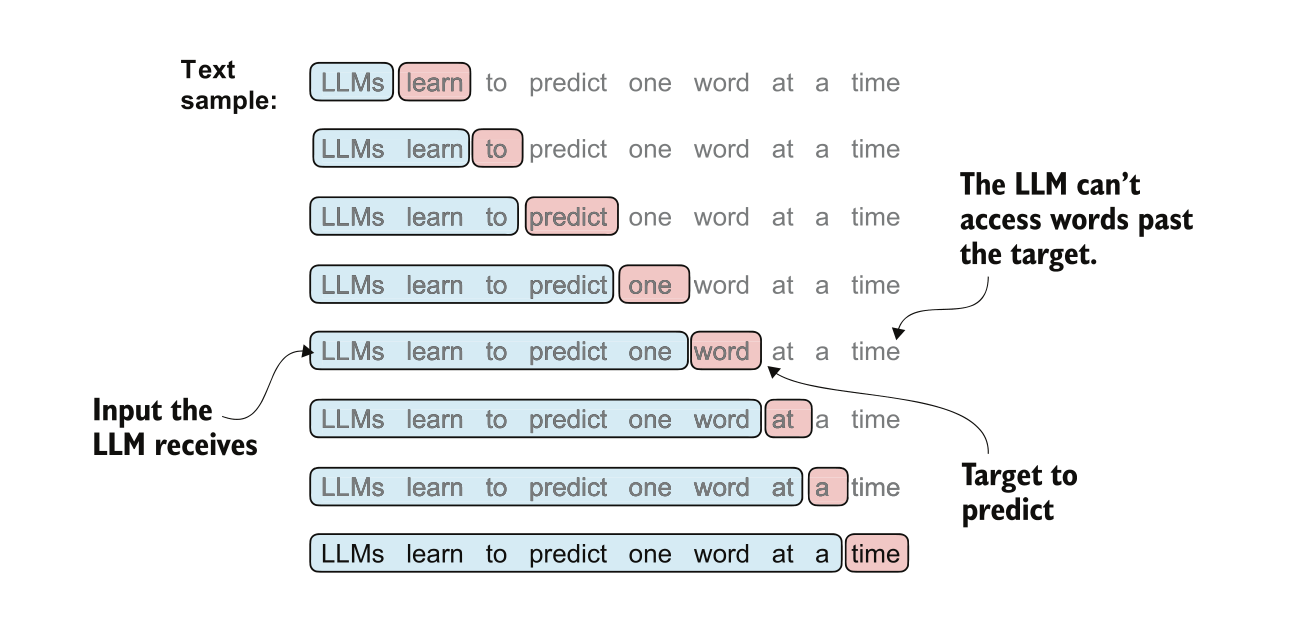
可能有人会问：LLM不是预测整个序列的联合概率分布的吗？为什么这里的表述都是条件概率的形式？我们前面在第二小节其实已经讨论过这个问题。看下面的图，会让这个过程更加清晰（图片出自[7]）：

上图表示训练过程中，输入进LLM的某一个batch中的其中一个sample（文本序列）：

LLMs learns to predict one word at a time

基于LLM的auto-regressive和causal attention机制，针对这个输入序列，模型实际上在同时做多个预测。可以拆解为：

• P(‘learn’|‘LLMs’)
• P(‘to’|‘LLMs learn’)
• P(‘predict’|‘LLMs learn to’)
• …
• P(‘time’|‘LLMs learns to predict one word at a’)

类似于前面第二小节做过的计算，这些项虽然都是条件概率，但全部乘起来，就（近似）等于整个序列的联合概率分布：

• P(‘LLMs learns to predict one word at a time’)

因此，可以说，预训练阶段的predict next token，实际上是在学习预测一个联合概率分布。

在SFT阶段，底层原理仍然是predict next token。但是，要预测的条件概率中多了一个instruction，即：P(output|input, instruction)。要对这个概率分布进行建模，传统的方法是设计新的模型架构，来接收和处理多出来的instruction。不过，按照现代LLM的思路，instruction也是文本序列，在这一点上它没有特殊性。因此，instruction应该可以和input合并到一起，基于某种prompt style格式化成一个更大的输入序列。

关于instruction作为输入序列一部分的一个有趣的例子是翻译。与Transformer不同，GPT模型最开始设计的时候，是基于decoder-only的架构。这种架构的目的是基于输入序列做predict next token，研究者并没有预期它可以像原始的Transformer那样能够执行翻译任务。但是，人们意外地发现它也具备了翻译的能力[7]。

小结

在本文中，我们解析了LLM背后的概率学原理，试图将基础的数学原理与LLM的实践结合起来。

一方面，LLM赖以运作的底层数学原理，与传统机器学习方法没有本质的不同；另一方面，它也是一项创举，开创了用一种简单的predict next token的机制，使用同一个模型架构来解决多种task的技术路线，为AGI的出现带来了一线曙光（虽然还有很多争议）。这种开创性的工作至少包括：

• 将模型设计成一个general的架构，不针对具体task修改模型架构。
• 训练数据规模大且尽量多样化，不局限于某个具体的domain或针对某个具体的task。
• 描述具体task的instruction也看成是文本序列，与input一起，做predict next token。

同时，我们也应该认识到，LLM的能力还远没有达到完美，存在诸如幻觉、推理能力 (Reasoning) 不够强等问题。理解它的原理与如何使用好它，是两个非常不同的问题。恰恰是因为LLM的不完美，我们才需要在应用层面做出更多的创新（不管是技术上的，还是产品上的）。

（正文完）

参考文献：

• [1] Christopher M. Bishop. 2006. Pattern Recognition and Machine Learning.
• [2] Bengio, Y., Ducharme, R., Vincent, P., and Jauvin, C. 2003. A neural probabilistic language model.
• [3] Ashish Vaswani, et al. 2017. Attention Is All You Need.
• [4] Alec Radford, et al. 2019. Language Models are Unsupervised Multitask Learners.
• [5] Tom B. Brown, et al. 2020. Language Models are Few-Shot Learners.
• [6] Michael A. Nielsen. 2015. A visual proof that neural nets can compute any function.
• [7] Sebastian Raschka. 2024. Build a Large Language Model (From Scratch).

其它精选文章：

• 技术变迁中的变与不变：如何更快地生成token？
• 用统计学的观点看世界：从找不到东西说起
• 从GraphRAG看信息的重新组织
• 企业AI智能体、数字化与行业分工
• 三个字节的历险
• 分布式领域最重要的一篇论文，到底讲了什么？
• 内卷、汉明问题与认知迭代
• 漫谈分布式系统、拜占庭将军问题与区块链
• 深度学习、信息论与统计学

原创文章，转载请注明出处，并包含下面的二维码！否则拒绝转载！
本文链接：http://zhangtielei.com/posts/blog-llm-probability.html
欢迎关注我的个人微博：微博上搜索我的名字「张铁蕾」。

---