OpenGL ES和坐标变换（一） - 铁蕾的个人博客

首页 > 移动开发 > 正文

OpenGL ES和坐标变换（一）
2017-09-18

相信做技术的同学，特别是做客户端开发的同学，都听说过OpenGL。要想对客户端的渲染机制有一个深入的了解，不对OpenGL了解一番恐怕是做不到的。而且，近年来客户端开发中对于图像和视频处理的需求，成上升趋势，要想胜任这些稍具「专业性」的工作，对于OpenGL的学习也是必不可少的。然而，OpenGL的学习曲线相对来说比较陡峭，尤其是涉及到一些计算机图形学方面的专业知识，不免会让很多人望而生畏。

要想熟练地掌握OpenGL，有两方面相关的知识是需要重点关注的。

一个是OpenGL的图形处理管线(graphics pipeline)，也就是图形渲染的整个过程包含哪些步骤，每个步骤的作用是什么，比如我们编写的vertex shader和fragment shader工作在哪些阶段，再比如depth testing (深度测试)、stencil testing (模板测试)，以及rasterization (光栅化)等等，分别起到什么作用；
另一个就是坐标变换，也就是vertex shader主要要完成的功能。如何将3D空间中的一个对象摆放到正确的位置，调整到正确的姿态，以及最终如何将3D坐标投射到2D的平面(一般来说是屏幕)上。

本文所要探讨的主题，将主要围绕上述第二个方面的知识，也就是坐标变换。这部分涉及到一点数学知识，显得更难理解一些，并且网上的资料也散落在各处，很少有系统而详尽的描述。严格来说，这部分理论知识并不完全属于OpenGL规范所规定的范围，但却与之有着非常密切的关系。接下来，就坐标变换这个主题，我会写一个小系列，由多篇技术文章组成，将坐标变换相关的资料整理在一起，并尽力用通俗易懂的语言表达出来，希望能为学习OpenGL和图像处理的同学扫清理论上的障碍。

本着理论联系实际的原则，我们将结合Android系统上的API介绍相关的理论。之所以选择Android环境，是因为上手简单，大部分程序员都能很快地跑起一个Android程序，并且OpenGL相关的编程环境在Android上是现成的，几乎不用太多的配置。在Android上，实际广泛使用的是OpenGL ES 2.0，它可以看成是OpenGL对应版本的一个子集。我们在接下来的讨论中，也以OpenGL ES 2.0为准。

另外，很多实际中的开发任务只涉及到2D图像的处理，而不会涉及3D的处理。使用OpenGL ES做2D的图像处理，确实处理流程会简化一些，然而，个人认为，搞清3D的渲染机制，对于理解整件事有至关重要的作用。理解了3D，便能理解2D，反之则不成立。而且，只有在3D的语境下，坐标变换的概念才能被完整地理解。因此，我们一开始便从3D开始，等介绍完3D空间中的坐标变换之后，我们再回到2D的特殊情况加以讨论。

一个例子程序

很多OpenGL的入门文章，都以画一个三角形开始。但是，对于讨论坐标变换这件事来说，画一个三角形的例子并不太合适，因为三角形是一个平面图形，对它应用了完整的坐标变换之后，会得到看似很奇怪的结果，反而让初学者比较迷惑。所以，本篇给出的例子程序画的是立方体(cube)。程序下载地址：

https://github.com/tielei/OpenGLESTransformationsDemo

下面是程序输出截图：

没错，程序画了三个立方体的木箱子，它们的位置、大小、角度各不相同。但实际上，上面的大木箱子和下面的小木箱子都是由中间的那个木箱子经过一定的坐标变换（缩放、旋转、平移）之后得到的。而中间的木箱子所在的位置是原始的位置，即世界坐标的原点处（世界坐标的概念我们马上就会介绍）。

在本篇中，我们先不过早地深入到代码细节，而是留到后面的文章再讨论。接下来，我们先把坐标变换的整个过程做一个概览。

坐标系和坐标变换

我们前面提到过，坐标变换的目标，简单来说，就是把一个3D空间中的对象最终投射到2D的屏幕上去（严格来说，OpenGL ES支持离屏渲染，所以最终未必是绘制到一个「可见」的屏幕上，不过在本文中我们忽略这一细节）。这也正是计算机图形学(computer graphics)所要解决的其中一个基础问题。当我们观察3D世界的时候，是通过一块2D的屏幕，我们真正看到的实际是3D世界在屏幕上的一个投影。坐标变换就是要解决在给定的观察视角下，3D世界的每个点最终对应到屏幕上的哪个像素上去。当然，对于一个3D对象的坐标变换，实际中是通过对它的每一个顶点(vertex)来执行相同的变换得到的。最终每个顶点变换到2D屏幕上，再经过后面的光栅化(rasterization)的过程，整个3D对象就对应到了屏幕的像素上，我们看到的效果就相当于透过一个2D屏幕「看到了」3D空间的物体（3D对象）。

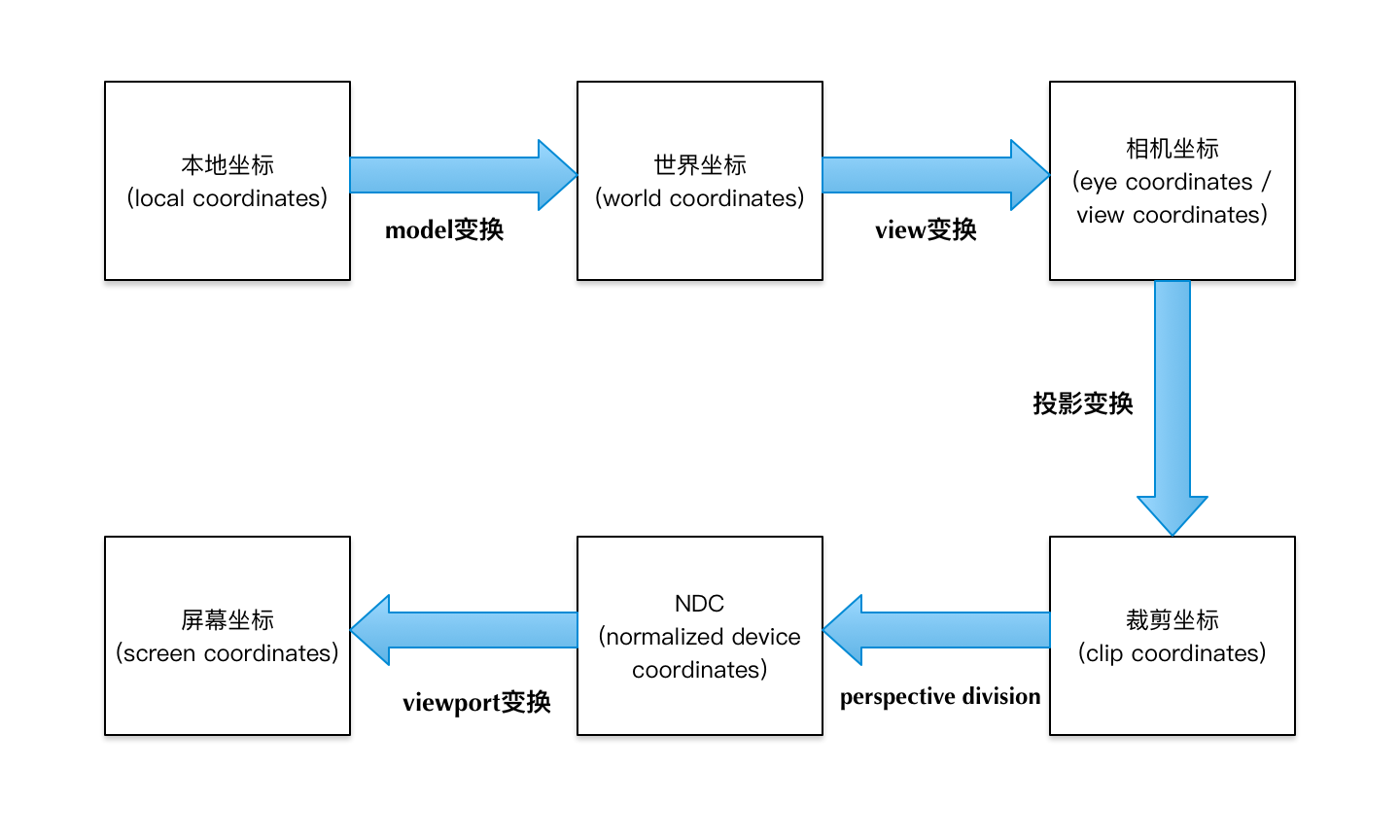
下面的图展示了整个坐标变换的过程：

我们先来简略地了解一下图中各个过程：

首先，一个3D对象的模型被创建（使用某种建模软件）出来之后，是以本地坐标(local coordinates)来表达的，坐标原点(0, 0, 0)一般位于3D对象的中心。不同的3D对象对应各自不同的本地坐标系(local space)。
3D对象的本地坐标经过一个model变换，就变换到成了世界坐标(world coordinates)。不同的对象经过各自的model变换之后，就都位于同一个世界坐标系(world space)中了，它们的世界坐标就能表达各自的相对位置。一般来说，model变换又包含三种可能的变换：缩放(scaling)、旋转(rotation)、平移(translation)。在计算机图形学中，一个变换通常使用矩阵乘法来计算完成，因此这里的model变换相当于给本地坐标左乘一个model矩阵，就得到了世界坐标。后边将要介绍的view变换和投影变换，也都对应着一个矩阵乘法。
在同一个世界坐标系内的各个3D对象共同组成了一个场景(scene)，对于这个场景，我们可以从不同的角度去观察。当观察角度不同的时候，我们眼中看到的也不同。为了表达这个观察视角，我们会再建立一个相机坐标系，英文可以称为camera space, 或eye space, 或view space。从世界坐标系到相机坐标系的转换，我们称之为view变换。当我们用相机这个词的时候，相机相当于眼睛，执行一个view变换，就相当于我们把眼睛调整到了我们想要的一个观察视角上。
对相机坐标执行一个投影变换(projection)，就变换成了裁剪坐标(clip coordinates)。在裁剪坐标系(clip space)下，x、y、z各个坐标轴上会指定一个可见范围，坐标超过可见范围的顶点(vertex)就会被裁剪掉，这样，3D场景中超出指定范围的部分最终就不会被绘制，我们也就看不到这些部分了。这个投影变换，是从3D变换到2D的关键步骤。之所以会有这么一步，是因为我们总是通过一个屏幕来观察3D场景（类似于透过一扇窗户观察窗外的景色），屏幕（窗户）不是无限大的，因此一定存在某些观察视角，我们看不到场景的全部。看不到的场景部分，就是通过这一步被裁剪掉的，这也是「裁剪」这一词的来历；另一方面，把3D场景投射到2D屏幕上，也主要是由这一步起的作用。另外值得注意的是，经过裁剪变换，3D对象的顶点个数不一定总是减少，还有可能被裁剪后反而增多了。这个细节我们留在后面再讨论。
裁剪坐标(clip coordinates)经过一个特殊的perspective division的过程，就变换成了NDC坐标(Normalized Device Coordinates)。这个perspective division的过程，跟齐次坐标有关，我们留在后面再讨论它的细节。由于这个过程在OpenGL ES中是自动进行的，我们不需要针对它来编程，因此我们经常把它和投影变换放在一起来理解。我们可以不太严谨地暂且认为，相机坐标经过了一个投影变换，就直接得到NDC了。NDC是什么呢？它才是真正的由OpenGL ES来定义的坐标。在NDC的定义中，x、y、z各个坐标都在[-1,1]之间。因此，NDC定义了一个边长为2的立方体，每个边从-1到1，NDC中的每个坐标都位于这个立方体内（落在立方体外的顶点在前一步已经被裁剪掉了）。值得注意的是，虽然NDC包含x、y、z三个坐标轴，但它主要表达了顶点在xOy平面内的位置，x和y坐标它们最终会对应到屏幕的像素位置上去。而z坐标只是为了表明深度关系，谁在前谁在后（前面的挡住后面的），因此z坐标只是相对大小有意义，z的绝对数值是多大并不具有现实的意义。
NDC坐标每个维度的取值范围都是[-1,1]，但屏幕坐标并不是这样，而是大小不一。以分辨率720x1280的屏幕为例，它的x取值范围是[0, 720]，y的取值范围是[0,1280]。这样NDC坐标就需要一个变换，才能变换到屏幕坐标(screen coordinates)，这个变换被称为视口变换(viewport transform)。在OpenGL ES中，这个变换也是自动完成的，但需要我们通过glViewport接口来指定绘制视口（屏幕）的大小。这里还需要注意的一点是，屏幕坐标(screen coordinates)与屏幕的像素(pixel)还不一样。屏幕坐标(screen coordinates)是屏幕上任意一个点的精确位置，简单来说就是可以是任意小数，但像素的位置只能是整数了。这里的视口变换是从NDC坐标变换到屏幕坐标，还没有到最终的像素位置。再从屏幕坐标对应到像素位置，是后面的光栅化完成的（光栅化的细节不在本文的讨论范围）。

为了更好地理解以上各个步骤，下面我们来看几张图。

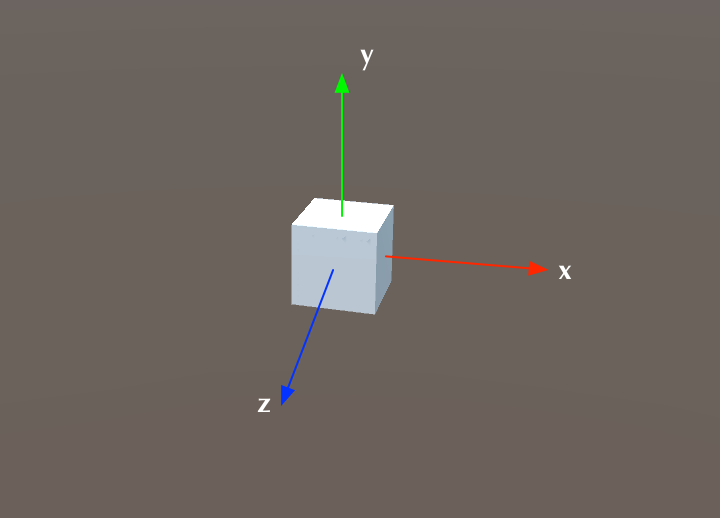
上面这张图展示的是本地坐标。3D对象是一个立方体，本地坐标的原点(0, 0, 0)位于立方体的中心。红色、绿色、蓝色的坐标轴分别表示x轴、y轴、z轴。

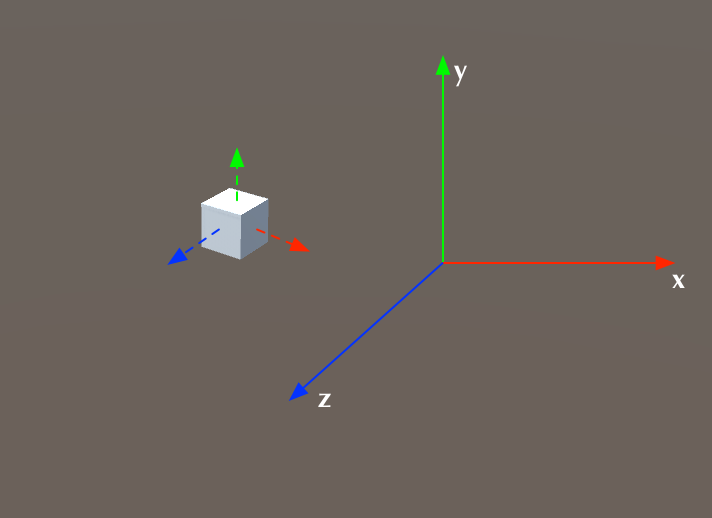
上面这张图展示的是世界坐标。可以这样认为，最初，世界坐标系和立方体的本地坐标系是重合的，但立方体经过了某些缩放、旋转和平移之后，两个坐标系不再重合。图中虚线表示的坐标轴，就是原来的本地坐标系。

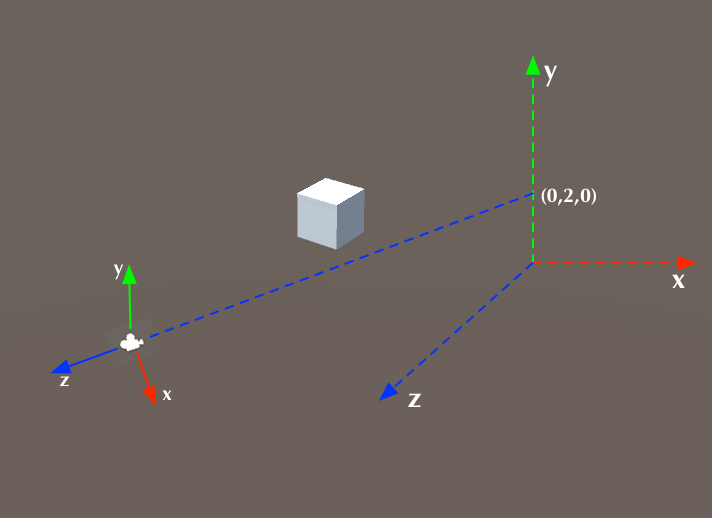
上面这张图展示的是相机坐标。左下实线表示的坐标轴即是相机坐标系，右边虚线表示的坐标轴是世界坐标系。相机坐标系可以看成是相机（或眼睛）看向3D空间中的某一点形成的一个观察视角，以上图为例，相机观察的方向正对着世界坐标系的(0,2,0)这一点。相机坐标系的原点正是相机（或眼睛）所在的位置。这里需要注意的一点细节是，按照OpenGL ES的定义习惯，相机坐标系的z轴方向与观察方向正好相反。也就是说，相机（或眼睛）看向z轴的负方向。

我们前面提到的view变换，指的就是在世界坐标系中的各个顶点(vertex)，经过这样一个变换，就到了相机坐标系下，也就是各个顶点的坐标变成了以相机坐标的值来表示了。

仔细观察的话，我们会发现，相机坐标系实际上可以看成是由世界坐标系经过旋转和平移操作得到的。这在后面我们还会详细讨论。

至此，我们已经转换到了相机坐标系下了。接下来是非常关键的一步变换，要将3D坐标（以相机坐标表示）投射到2D屏幕上。如前所述，这个变换是通过投影变换(projection)得到的。为了使得投射到2D屏幕上的图像看起来像是3D的，我们需要让这个变换满足人眼的一些直觉。根据实际经验，我们眼中看到的东西，离我们越远，显得越小；反之，离我们越近，显得越大。就像我们正对着一列铁轨或一个走廊看过去的那种效果一样，如下图：

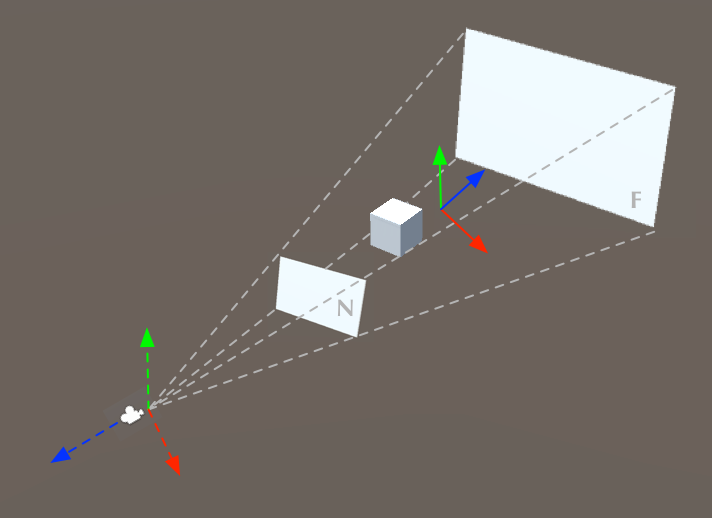
所以，投影变换也要保持这种效果。经过投影变换后，我们就得到了裁剪坐标，在此基础上再附加一个perspective division的过程，就变换到了NDC坐标。像前面所讲的一样，perspective division的细节我们先不追究，我们暂且认为相机坐标经过了投影变换就得到了NDC坐标。这个投影的过程，是通过从相机出发构建一个视锥体(frustum)得到的，如下图所示：

上图中，从相机所在位置（也就是相机坐标系原点）沿着相机坐标系的z轴负方向望出去，同时指定一个近平面(N)和远平面(F)，在两个平面之间就截出一个视锥体。它由6个面组成，近平面(N)和远平面(F)分别是前后两个面，另外它还有上下左右四个面。其中，近平面(N)对应着最终要投影的2D屏幕。落在视锥体内部的顶点坐标，最终将投影到2D屏幕上；而落在视锥体外部的顶点坐标，则被裁剪掉。而且，落在视锥体内部的3D对象，它的位置越是靠近近平面，这个3D对象在近平面上的投影越大；相反越是远离近平面，则投影越小。

以视锥体中的某点为原点，建立一个坐标系，就得到了NDC坐标，也就是上图中位于右上部的实线红、绿、蓝坐标轴。视锥体的6个面正好对应着NDC坐标每个维度的最大取值（-1和1）。

有两个细节需要注意一下：

NDC坐标系的原点并没有在视锥体的中心。这主要是因为，在从相机坐标变换到NDC坐标的过程中，z轴上是一个非线性的对应关系。这个细节我们在后面讨论投影变换的计算时再详细说明。
前面的本地坐标系、世界坐标系、相机坐标系，都是属于右手坐标系(right-handed coordinate system)。只有NDC坐标系是左手坐标系(left-handed coordinate system)。