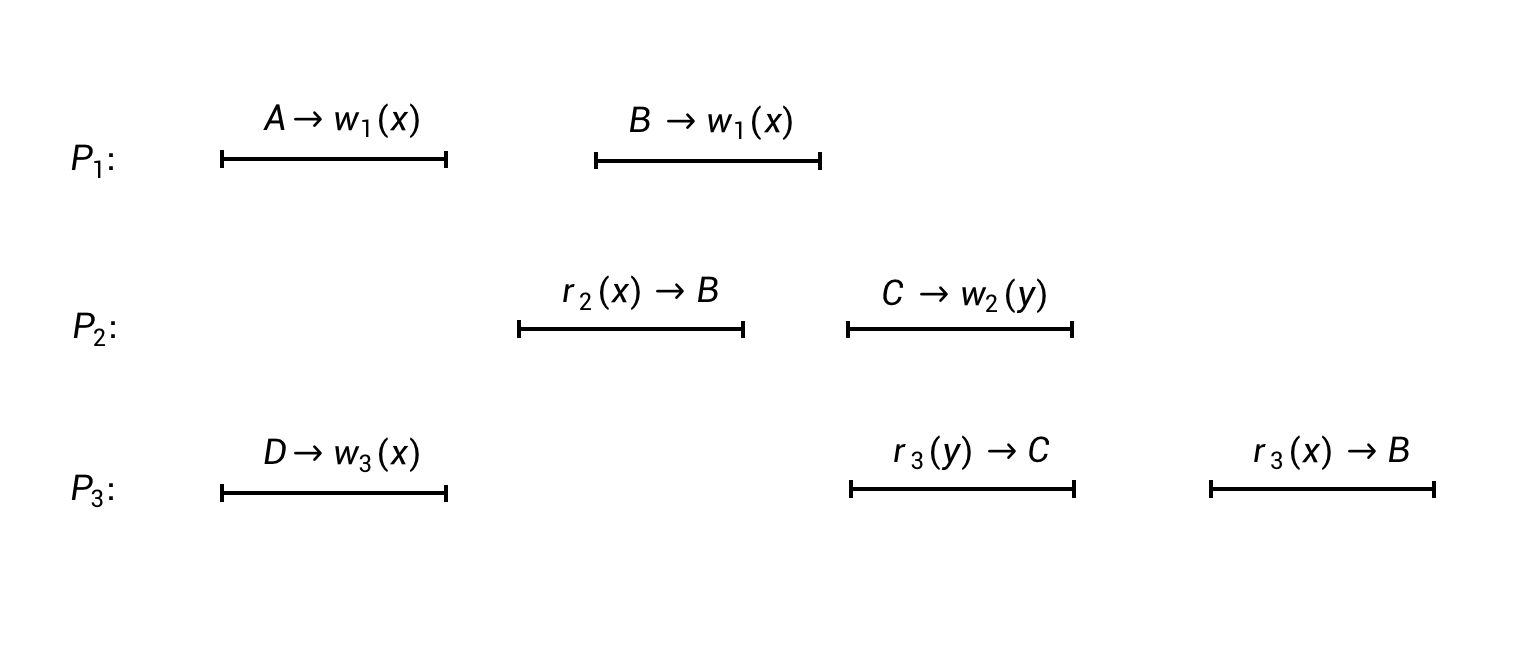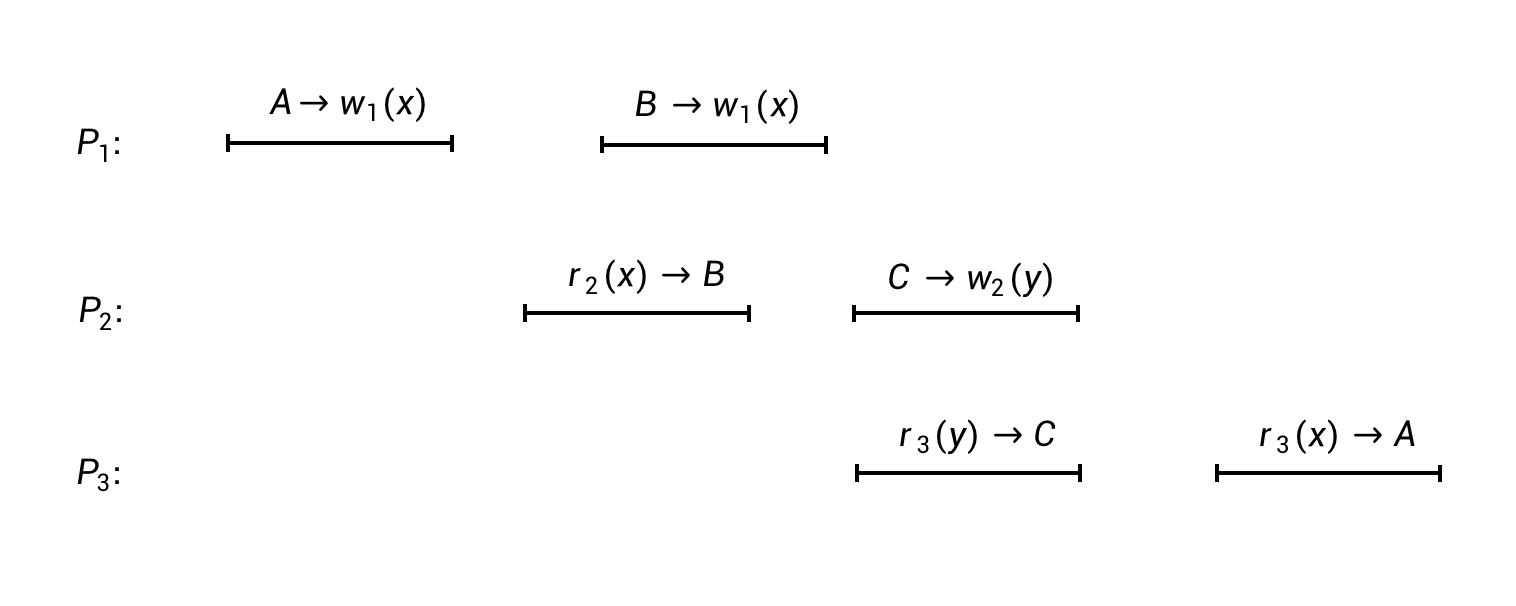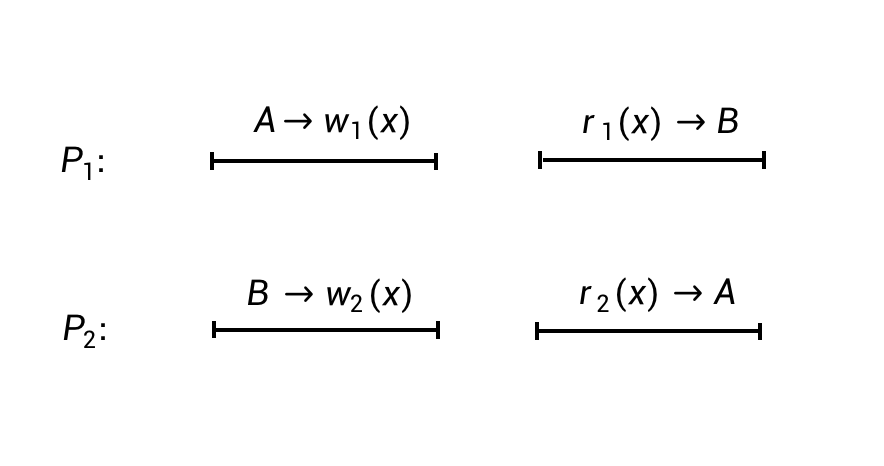条分缕析分布式：因果一致性和相对论时空

首页 > 分布式 > 正文

条分缕析分布式：因果一致性和相对论时空
2020-12-22

在上一篇文章《条分缕析分布式：浅析强弱一致性》中，我们重点讨论了顺序一致性、线性一致性和最终一致性这几个概念。本文我们将继续深入，详细探讨另一种一致性模型——因果一致性，并在这个过程中逐步逼近分布式系统最深层的事件排序的本质。沿着这个方向，如果我们走得稍微再远一点，就会触达我们所生活的这个宇宙的时空本质，以及因果律的本质（这才是真正有意思的地方，希望你能一口气读到最后）。

回到现实，《Designing Data-Intensive Applications》[1]一书的作者在他的书中提到，基于因果一致性构建分布式数据库系统，是未来一个非常有前景的研究方向。而且，估计很少有人注意到，我们经常使用的ZooKeeper，其实就在session维度上提供了因果一致性的保证[2]。理解「因果一致性」的概念，有助于我们对于分布式系统的认识更进一层。

为什么要考虑因果一致性？

结合上一篇文章的讨论，我们再把一致性模型的来历简单梳理一下。

早期的分布式系统设计者，为了让使用系统的开发者能够以比较简单的方式来使用系统，希望分布式系统能提供单一系统视图 (SSI，single-system image)[3]，即系统“表现得就好像只有一个单一的副本”。线性一致性和顺序一致性就是沿着这个思路设计的。满足线性一致性或顺序一致性的系统，对读写操作的排序呈现全局唯一的一种次序。

然而，系统为了维持这种全局排序的一致性是有成本的，必然需要在副本节点之间做很多通信和协调工作。这降低了系统的可用性（availability）和性能。于是，在一致性、可用性、系统性能之间进行权衡的结果，就是降低系统提供的一致性保障，转向了最终一致性[4]。

不过最终一致性提供的一致性保障是如此之弱，它放弃了所有的safety属性（具体讨论见上一篇文章）。这给系统的使用带来了额外的困难。面向最终一致性系统进行编程，需要随时关注数据不一致的情况。加州大学伯克利分校在2013年发表了一篇非常不错的文章[3]，对于如何在最终一致性系统上构建应用，进行了非常深入的研究。文章指出了两种思路：

针对可能出现的数据不一致情况实施补偿措施 (compensation)。这需要在分布式系统之上的应用层面进行额外的处理，是非常容易出错且费时费力的。
基于CALM定理和CRDTs，完全消除补偿操作。但这样做其实限制了应用编程能够使用的操作类型，也就限制了系统能力。

以上两种思路都涉及到了大量细节，我们不打算在这里深入讨论，有兴趣的读者可以仔细去阅读论文[3]。

总之，为了提高系统可用性和系统性能，人们放弃了强一致性，采取了几乎最弱的一类一致性模型（最终一致性），但也同时牺牲了系统的能力或系统使用的便利性。那么，到底有没有必要一定采取这么「弱」的一致性模型呢？有没有可能在最终一致性的基础上增加一点safety属性，提供稍强一点的一致性，但同时也不至于对系统可用性和性能产生明显的损害呢？

基于最新的研究，这是有可能的。这个问题的答案就是本文接下来要讨论的因果一致性 (causal consistency)。

德克萨斯大学奥斯汀分校在2011年的一项研究表明[5]：

不存在比因果一致性更强的一致性模型，能够在网络分区的情况下仍然可用。
在一个永远保持可用且单程收敛 (always-available, one-way convergent) 的系统里，因果一致性是可以被实现出来的。

因果一致性的直观解释

因果律是这个世界最基础的规律，物理法则决定了我们总是先看到事物的「因」，后看到事物的「果」。对于一个分布式系统来说，在数字世界中保持这种因果关系，当然也是一个最基本的要求。

为了能比较通俗地理解因果一致性，我们这里引用一个假想的实例（来自论文[6]）。假设Billy是一个小男孩，Sally是他的妈妈。下面的故事发生在一个类似Facebook的社交网站上：

有一天，Billy失踪了。Sally找不到他的儿子，很着急，于是在社交网站上发布了一条状态：“我儿子Billy丢了！”
过了一会，Sally突然接到了儿子的电话。Billy告诉妈妈，他跑到朋友家玩去了。Sally长出一口气，又重新修改了刚才发布的状态：“谢天谢地，虚惊一场！Billy原来是跑出去玩了。”
Sally的一个朋友，叫James，看到了她发的最新的状态，在社交网站上回复了她：“太好了，总算松了一口气！”

假如这家社交网站的数据库系统没能保证因果一致性，那么我们就可能看到比较奇怪的事件次序。假设Sally的另外一个朋友，叫Henry，也在浏览这个社交网站。可能由于系统延迟，数据还未收敛到一致的状态，Henry可能会看到Sally发的第一条状态和James的回复，但却看不到Sally发的第二条状态。于是，在Henry看来：

Sally说：“我儿子Billy丢了！”
James回复：“太好了，总算松了一口气！”

Henry可能会错误地认为，James满心希望Sally的儿子丢了（James肯定是恨透了Sally）！

之所以发生这样的问题，就是因为因果倒置了。考虑两个事件：事件A，Sally发布第二条状态（称自己的儿子找到了）；事件B，James回复Sally表示安慰。显然，事件B是由事件A引发的，也就是说，事件A是事件B的「因」，事件B是事件A的「果」。但在Henry看来，却只看到了事件B，没有看到事件A，这违反了因果规律。（当然，这个例子隐藏了很多具体实现细节，你可能会产生一些疑问，但不妨碍我们讨论事件的因果关系）

这里需要注意，如果分布式系统是满足线性一致性或者顺序一致性的，那么是不会发生这样的问题的。因为线性一致性和顺序一致性是能够保持因果关系的（下一章节我们还会继续讨论这个问题）。而只是满足最终一致性的系统，是没法总是保持因果关系的。但是，如果一个系统满足因果一致性，那么我们可以放心地认为，事件的因果关系是能够得到保证的。

现在，让我们来尝试对因果一致性进行定义。我们先采取一种不那么严格，但比较直观的说法（下个章节再进行精确定义）。因果一致性遵守下面三条规则：

单进程写操作有序。
“writes follow reads”规则。
因果关系可传递。

我们来分别解释一下：

单进程写操作有序，指的是一个进程的多个写操作（可能是针对不同的数据对象的），在所有进程看来都是遵循同样的执行顺序。对应到前面的例子中，Sally的所有朋友都会看到，Sally是先发了一条状态“我儿子Billy丢了！”，然后又发了第二条状态“谢天谢地，虚惊一场！Billy原来是跑出去玩了。”这条规则保证了没有人是先看到第二条状态然后才看到第一条状态的。对于这个次序的保证也是因果性的一种体现。
“writes follow reads”指的是，假设第一个进程先读取到了数据对象x=5，后写入了另一个数据对象y=10，然后第二个进程读到了y=10，那么接下来如果这个进程读取数据对象x的值，那么不能读到一个比x=5更旧的值。这条规则在不同进程的不同数据对象之间建立了因果关联。对应到前面的例子中，James看到了Sally发的最新状态：“谢天谢地，虚惊一场！Billy原来是跑出去玩了。”（相当于读到了x=5），然后回复说：“太好了，总算松了一口气！”（相当于写入了y=10），再然后Henry看到了James的回复内容（相当于第二个进程读到了y=10），这时候站在Henry的视角上看Sally发布的状态，他不能比James看到的数据版本更旧。前面的例子中出现的问题就在于，Henry比James看到了更旧的一个数据版本：“我儿子Billy丢了！”，致使因果关系混乱了。
因果关系是具有传递性的。如果操作A和操作B在因果关系上满足先后次序，而且操作B和操作C在因果关系上也满足先后次序，那么A和C在因果关系上必然是满足先后次序的。

因果一致性的精确定义

在前一章节我们讨论了因果一致性的直观解释，但我们还需要一个精确的定义。这样对于一个具体的包含读写操作的并发执行过程来说，我们才能知道如何判定它是否满足因果一致性。

我们采用上一篇文章的表示方法，还是先通过一个例子来看一个并发执行过程，如下图：

图中线段上面的符号表示具体的读写操作：

A –> w_i(x)，表示一个写操作：第i个进程向数据对象x写入了值A。
r_i(x) –> A，表示一个读操作：第i个进程从数据对象x中读到了值A。

这个图表达了3个进程（P₁、P₂和P₃）对于数据存储的读写执行过程。它是否满足因果一致性呢？

跟线性一致性和顺序一致性的定义一样，因果一致性也是表达了系统对于读写操作的某种排序规则。为此我们首先需要定义清楚一个关键概念——因果顺序 (causality order)，它表明了两个不同操作之间的排序是怎样规定的。

因果顺序的定义：如果两个操作o₁和o₂满足下面三个条件之一，那么它们就是满足因果顺序的，记为o₁→o₂：

(1) o₁和o₂属于同一个进程，且o₁在o₂前面执行。
(2) o₁是个写操作，o₂是个读操作，且o₂读到的值是由o₁写入的。
(3) 存在一个操作o’满足o₁→o’→o₂。

结合上图的例子，我们解释一下这三个条件：

(1) 同一个进程内部先后执行的两个操作，不管他们是读操作还是写操作，都是满足因果顺序的。比如上图中P₁进程的 A –> w₁(x) 和 B –> w₁(x) 两个操作就是满足因果顺序的；P₂进程的 r₂(x) –> B 和 C –> w₂(y) 也是满足因果顺序的。这一条件表明，因果顺序遵从了进程的执行顺序。
(2) 如果一个读操作读到的值是由另一个写操作写入的（肯定是针对同一个数据对象），那么不管它们是不是属于同一个进程，这个写操作和读操作就是满足因果关系的。比如上图中的 B –> w₁(x) 和 r₂(x) –> B 就是满足因果顺序的；C –> w₂(y) 和 r₃(y) –> C 也是满足因果顺序的。这个条件反映了读写操作之间的因果依赖关系。
(3) 这个条件表明因果顺序“→”满足传递关系 (transitive relation)。

从因果顺序的定义中，我们还能得到两个重要的结论：

因果顺序是一种偏序关系。所谓偏序关系，就是说只有一部分操作是可以按照因果顺序进行比较的，而有一些操作之间是不能比较的。比如上图中的 A –> w₁(x) 和 D –> w₃(x) 这两个操作之间的关系，就不符合因果顺序三个条件中的任何一个。r₂(x) –> B 和 D –> w₃(x) 之间也同样如此，它们之间不存在因果顺序。这具有很深刻的物理学和哲学内涵，因为现实世界的事件之间的因果关系就是偏序的（先不展开讨论）。分布式系统里对于读写操作之间的这种因果顺序的定义，正是对现实世界中这种现象的一种刻画。
因果顺序不能有循环依赖。假如操作o₁→o₂→o’→…→o₁，由传递关系就应该有：o₁→o₁。这表示一个操作是它自己的「因」，这是荒谬的。换句话说，如果把因果顺序用一个图来表示，那么它应该是一个有向无环图 (directed acyclic graph)。

现在基于因果顺序的定义，我们可以给出因果一致性的定义了。

因果一致性定义[7]：在一个并发执行过程中，站在其中任意一个进程P_i的视角上，考虑这个进程的所有读、写操作和所有其它进程的所有写操作（注意不包含读操作），得到一个操作序列。如果站在任意一个进程的视角上得到的这个操作序列都能够重排成一个线性有序的序列，并且该序列满足以下两个条件，那么这个并发执行过程就是满足因果一致性的：

条件I：重排后的序列中每一个读操作返回的值，必须等于前面对同一个数据对象的最近一次写操作所写入的值。
条件II：重排后的序列遵从前面定义的因果顺序“→”。

对比上一篇文章中的顺序一致性定义，因果一致性的定义有两个不同：

顺序一致性是对所有进程的所有读写操作进行统一的重排，而因果一致性是站在每个进程的视角各自进行局部重排。这表示顺序一致性要求系统的所有进程都对操作排序达成一致的看法，而因果一致性允许每个进程对操作的排序有不同的看法。
因果一致性与顺序一致性的条件II不同。顺序一致性的条件II只是要求遵从进程的执行顺序，而因果一致性则有更强的要求——遵从因果顺序（而进程的执行顺序只是因果顺序的一部分）。

以前面图示的并发执行过程为例，我们先以P₁的视角，需要考虑把P₁的所有读写操作和P₂、P₃的所有写操作进行重排，可以得到如下的有序序列：

D –> w₃(x)
A –> w₁(x)
B –> w₁(x)
C –> w₂(y)

再以P₂的视角，需要考虑把P₂的所有读写操作和P₁、P₃的所有写操作进行重排，可以得到如下的有序序列：

D –> w₃(x)
A –> w₁(x)
B –> w₁(x)
r₂(x) –> B
C –> w₂(y)

最后以P₃的视角，需要考虑把P₃的所有读写操作和P₁、P₃的所有写操作进行重排，可以得到如下的有序序列：

D –> w₃(x)
A –> w₁(x)
B –> w₁(x)
C –> w₂(y)
r₃(y) –> C
r₃(x) –> B

我们可以依次检查三个重排序列，会发现因果一致性的 条件I和条件II都是满足的（留给读者自己去检查，有疑问可以在评论区回复），所以前面图中的并发执行过程是满足因果一致性的。

你可能会觉得因果一致性的定义有些复杂，那么它的设计初衷是什么呢？我们通过分析两个问题来做初步的解读：

为什么因果一致性是站在各个进程的视角对部分操作进行排序，而不是对所有进程的操作进行全局排序？这是因为，因果顺序是一种偏序关系，这就允许站在不同进程的视角去观察各自所关心的部分操作，从而得到不同的观察结果（排序序列）且同时不违反因果律。假如因果顺序不是一种偏序，而是一种全局关系，那么就可以把所有操作按照同一个次序排序起来，那就变成跟顺序一致性一样了，每个进程也可以看到完全一样的排序序列了。所以说，这里隐含着一个结论：因果一致性是比顺序一致性更弱的一类一致性模型，而顺序一致性也意味着遵从了因果一致性。另外，也只有当站在不同进程的视角有不同的观察结果时，才可能在发生网络分区的时候，同时提供可用性。想象当一个节点同系统其它部分隔开了，这个节点不需要等待与其它节点联系，仍然可以使用旧版本的数据提供服务，同时不违反因果顺序即可。而如果像顺序一致性或者线性一致性那样，维持一个统一的全局排序，则需要在各个节点之间充分交换完数据才能达成一致。
为什么站在一个进程的视角要考虑所有其它进程的写操作呢？因为对于因果顺序来说，所有写操作都是潜在的「因」，而当前进程的读操作则代表了它的「看法」。进程的局部看法的形成，需要考虑所有的「因」，才能保证不违反因果律。

最后我们再来看一下，前一章节提到的因果一致性遵守的三条规则，是不是在因果一致性的定义中包含了：

单进程写操作有序。因为每个进程进行局部重排的时候，都把所有进程的写操作考虑进去了，所以任何一个进程的多个写操作，在所有进程看来都是遵循同样的执行顺序。比如前面例子中P₁的两个操作 A –> w₁(x) 和 B –> w₁(x)，在三次重排序列中都能保持次序。
“writes follow reads”规则。隐含在因果顺序的前两个条件里面。在前面例子中，进程P₂先是读取到了x=B，后写入了y=C，然后进程P₃先是读到了y=C，接下来进程P₃读取x的值，不能读到一个比x=B更旧的值（满足）。
因果关系可传递。隐含在因果顺序的第三个条件里。

作为对比，下图是一个违反了“writes follow reads”的例子（因此不满足因果一致性）：

分布式系统事件排序

因果一致性的概念[7]，是受到Lamport的经典论文[8]的启发而设计出来的。Lamport在1978年发表的经典论文《Time, Clocks, and the Ordering of Events in a Distributed System》，经常被认为是分布式领域中最重要的一篇论文。这篇论文定义了分布式系统中不同事件之间的一种偏序关系，称为“happened before”关系，即是对因果关系的一种刻画。

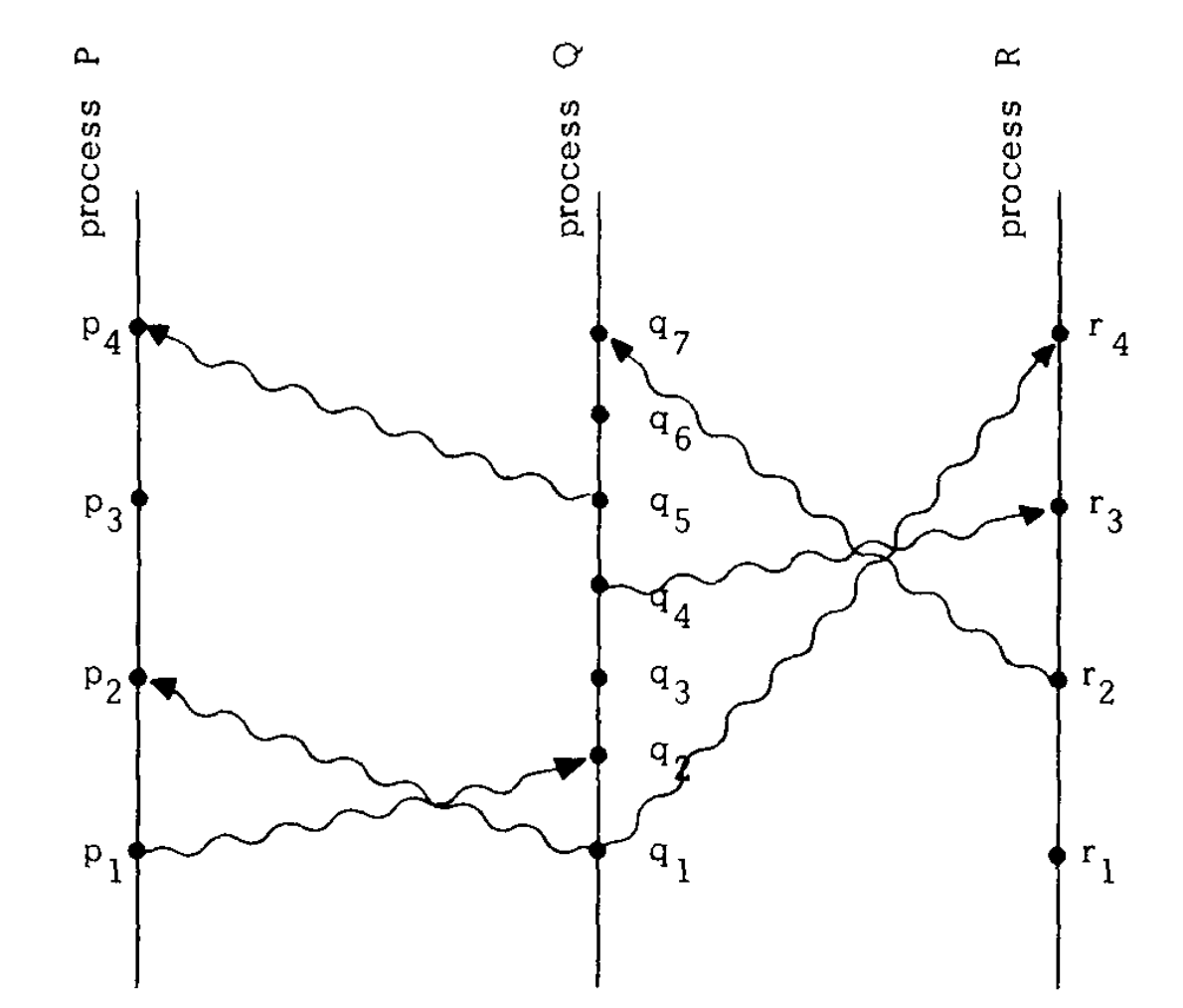
Lamport定义了一种由不同进程组成的分布式系统模型，进程之间通过收发消息来传递信息。如下图：

在上图中，我们尝试对消息发送事件和消息接收事件进行排序（注意图中自下而上时间递增）。“happened before”关系也是用符号“→”来表示。

在进程Q内部，q₂表示一个消息接收事件，q₄表示另一个消息发送事件，q₂排在q₄前面执行，所以q₂→q₄。
p₁和q₂分别表示同一个消息的发送事件和接收事件，所以p₁→q₂；同理，q₄→r₃。
“happened before”满足传递关系。由p₁→q₂，q₂→q₄和q₄→r₃，可以推出p₁→r₃。

以上三种情况，与我们前面讨论的因果顺序定义中的三个条件，基本一一对应。因果一致性的概念应用在分布式存储系统上，相当于将“happened before”关系应用在了读写操作之上。

可以看出，这里的“happened before”关系，也是一种偏序关系。比如p₁和q₁两个事件就是无法比较的，q₄和r₂也是无法比较的。无法比较的两个事件之间不满足“happened before”关系。

因果一致性的难以理解之处

经过以上的讨论，相信你已经对因果一致性有了初步的理解了。现在我们来看一个稍显奇怪的例子（下图的例子出自论文[7]）。

上图表达了两个进程的并发执行过程。它是满足因果一致性的，因为站在进程P₁和P₂的视角，都能得到一个局部合理的排序（满足因果顺序）。

站在P₁视角，有：

A –> w₁(x)
B –> w₂(x)
r₁(x) –> B

站在P₂视角，有：

B –> w₂(x)
A –> w₁(x)
r₂(x) –> A

以上这些分析完全符合因果一致性的定义。但是，仔细看这个例子，如果接下来没有任何进程对数据对象x进行写操作了，那么P₁永远读到的是x=B，而P₂永远读到的是x=A。这似乎有些不可思议。

发生这个现象的原因在于，进程P₁和P₂对于两个写操作的排序，「看法」不一致：

在P₁看来，A –> w₁(x)发生在B –> w₂(x)前面。
在P₂看来，B –> w₂(x)发生在A –> w₁(x)前面。

这就如同相对论难以理解一样：不同参照系的观察者对于不同事件的先后顺序，可能产生不同的看法。实际上，分别站在进程P₁和P₂的视角上，它们看到的都没有什么矛盾。矛盾发生在我们站在全局视角去看的时候。

假设躲在进程P₁和P₂背后的两个用户，通过系统外的通信方式进行了交流，那么他们就会发现这个奇怪之处：他们竟然对于同一个数据对象x读到的值不同！但是站在因果一致性的分布式系统内部来看的话，不应该发生这种情况，因为进程之间的沟通，都应该在系统内发生。所谓发生在系统内的进程之间的沟通，必定是通过进程对于数据对象的读写操作进行的。如果进程P₁或P₂对数据对象x进行了写操作，那么它们就有机会对数据对象x的值达成同样的看法；或者很不走运，永远也达不成同样的看法，但它们如果不借助系统外的手段永远也发现不了这种不同（还是不违反因果律）。

顺便提一句，如果要保证在系统外发生的因果联系也能在系统内永远被遵守，那么就要借助于Lamport在他的论文中提到的Strong Clock Condition了。

更进一步

我们前面提到，因果一致性对于分布式系统读写操作事件的排序，是对现实世界的事件之间因果关系的一种刻画。理解的难点在于，在我们所生活的这个宇宙中，事件之间的时间次序，只是一种偏序关系；对应的，事件之间的因果关系，也是一种偏序。

在牛顿的绝对时空观中，时间是以某个固定速率向前流逝的绝对量，而不管我们站在哪个参照系的视角上。由此带来的推论是，宇宙中发生的任何一个事件，都可以根据它们发生的绝对时间点进行先后排序。也就是说，在绝对时空中的事件之间的排序是一种全序关系，任何两个事件都能比较先后。发生在前面的事件就有可能影响后面的事件，从而产生因果关系。试想一下，就在你读到这里的几秒之前，三体星系上发生了某个重大事件，按照绝对时空观的观点，它也可能对现在的你产生了影响。你大概会同意，这是不可能的，因为三体星系即使以最快的速度向地球传递信息，也要在4年之后才能到达。

而在爱因斯坦的相对论中，这个问题就得到了解决。时间不再是一个绝对的量。不同参照系看到的时间流速可以快慢不同，甚至对两个事件的先后次序可以看法不同。但是，对于可能互相产生影响的事件，它们之间的先后次序，不管在什么参照系上看到的都应该是相同的，否则就违反了因果律。实际上，在相对论的时空中，结论是这样的：

一个事件，和在它的「未来光锥」之内的任何其它事件，都是有偏序关系的。它们之间的先后次序，不管在什么参照系上看到的都应该是相同的。
一个事件，和在它的「未来光锥」之外的其它事件，是没有偏序关系的（也就不可能产生因果关系）。站在不同参照系上看这样的两个事件，它们的先后次序可能不同。

回到我们的分布式系统。一个分布式系统自成宇宙，它是对现实世界的一种刻画。分布式系统由不同的进程组成，而不同的进程分布在不同的空间，每个进程可以看成一个单独的参照系。因果一致性，本质上就是按照我们对于相对论宇宙的认识来进行系统建模的，这也是它的合理性的根基。然而，分布式系统毕竟只是一个模拟系统，它是服务于系统外的现实世界的。而在现实世界中，我们还可以有额外的传递信息的方式，这相当于在分布式系统自成体系的这个「宇宙」之外，可能存在更快的传递信息的维度。所以说，分布式系统只依靠自己的逻辑，是无法与现实世界完全达成一致的。而要做到对现实的完美刻画，就一定需要考虑现实世界的实时时钟（可以从Lamport的Strong Clock Condition入手）。

到这里，我们已经触达到分布式系统（也包括这个宇宙时空）最深层的本质问题了。相信在这样的逻辑框架下，任何分布式系统的相关问题，都能很容易找到它在整个体系中的逻辑位置。至此，我们也完成了分布式一致性这个话题的「三部曲」了。其它两篇参见：

当然，分布式相关的话题还远没有结束，还有更多有意思的问题等着我们去探究。

（正文完）

参考文献：

[1] Martin Kleppmann,《Designing Data-Intensive Applications》, 2017.
[2] Martin Kleppmann, “Please Stop Calling Databases CP or AP”, 2015.
[3] Peter Bailis, Ali Ghodsi, “Eventual Consistency Today: Limitations, Extensions, and Beyond”, 2013.
[4] Werner Vogels, “Eventually Consistent”, 2008.
[5] Prince Mahajan, Lorenzo Alvisi, Mike Dahlin, “Consistency, Availability, and Convergence”, 2011.
[6] Peter Bailis, Ali Ghodsi, et al, “Bolt-on Causal Consistency”, 2013.
[7] Mustaque Ahamad, Gil Neiger, James E. Burns, et al, “Causal Memory: Definitions, Implementation and Programming”, 1994.
[8] Leslie Lamport, “Time, Clocks, and the Ordering of Events in a Distributed System”, 1978.

其它精选文章：

原创文章，转载请注明出处，并包含下面的二维码！否则拒绝转载！
本文链接：http://zhangtielei.com/posts/blog-distributed-causal-consistency.html
欢迎关注我的个人微博：微博上搜索我的名字「张铁蕾」。

上篇：条分缕析分布式：浅析强弱一致性

下篇：分布式领域最重要的一篇论文，到底讲了什么？