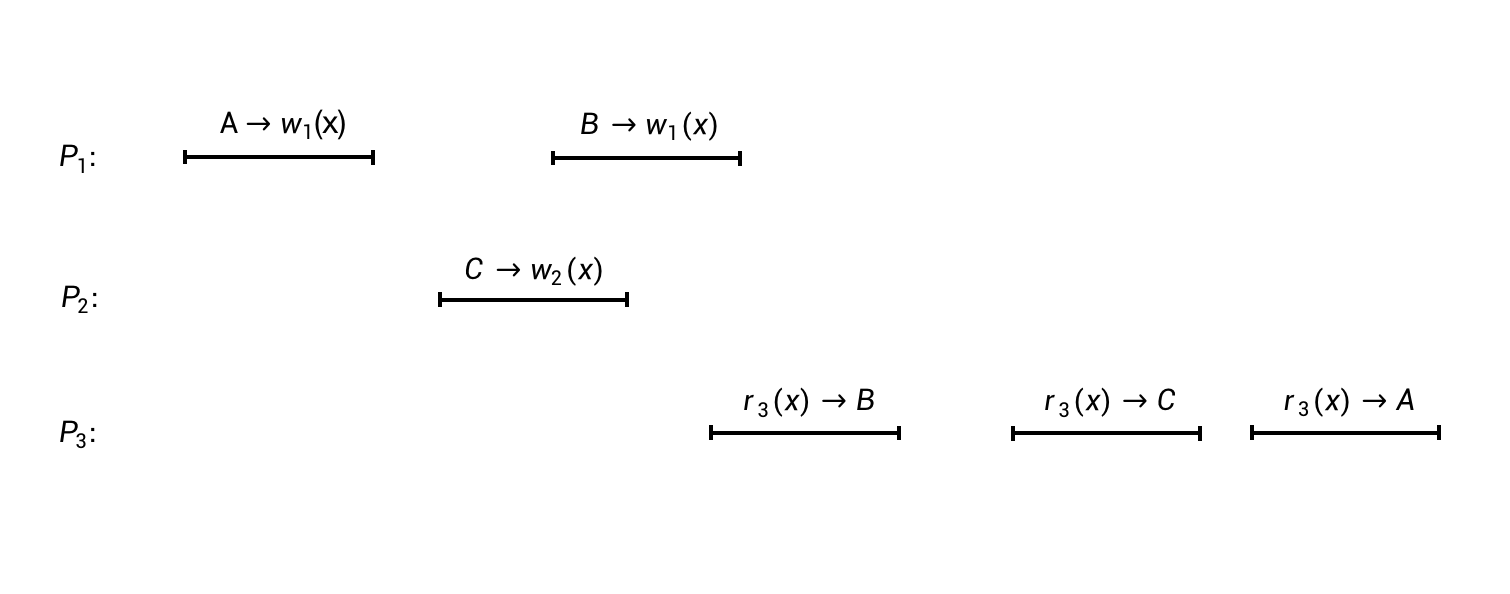条分缕析分布式：浅析强弱一致性

首页 > 分布式 > 正文

条分缕析分布式：浅析强弱一致性
2020-10-04

当前这篇文章至少比计划拖后了两个月。在上一篇文章《条分缕析分布式：到底什么是一致性？》中，我们仔细辨析了「一致性」相关的几个容易混淆的概念。而在本文中，我们会沿着逐步深入的思路，跟大家继续讨论顺序一致性、线性一致性、最终一致性等几个概念。

为了避免产生歧义，我们先明确一下这几个概念的英文表达：

顺序一致性的英文是：sequential consistency。
线性一致性的英文是：linearizability。实际上，它就是CAP定理中的C，我们在上一篇文章中已经提到过。
最终一致性的英文是：eventual consistency。

在进行详细的技术性讨论之前，我们先把本文要讨论的几个重点问题和结论列出如下：

线性一致性和顺序一致性，属于分布式系统的一致性模型 (consistency model)。这代表了分布式系统的一个非常非常重要的方面。
通常人们把线性一致性称为「强一致性」，把最终一致性称为「弱一致性」，但线性一致性和最终一致性其实存在本质的区别。严格来说，它们并不是一个范畴的概念。
一致性模型之间的「强弱」比较，是一个相对的概念。比如，线性一致性是比顺序一致性更强的一致性模型。当然，除了线性一致性和顺序一致性，也存在其它一些一致性模型（其中很多都比顺序一致性要弱）。
满足线性一致性的系统，也必定满足顺序一致性，但反过来不一定。这是由一致性模型之间的强弱关系决定的。

下面，我们就开始详细的解析。

一致性模型的来历

我们之所以使用分布式系统，无非是因为分布式系统能带来一些「好处」，比如容错性、可扩展性等等。为了获得这些「好处」，分布式系统实现上常用的方法是复制 (replication) 和分片 (sharding)。而我们将要讨论的一致性模型 (consistency model)，主要是与复制有关。因此这里我们先关注一下复制的机制。

复制指的是将同一份数据保存在多个网络节点上。而保存同一份数据拷贝的节点，被称为副本 (replica)。复制带来的具体「好处」主要是体现在两个方面：

容错 (fault tolerance)。即使某些网络节点发生故障，由于原本保存着在故障节点上的数据在正常节点上还有备份，所以整个系统仍然可能是可用的。这也是我们期待分布式系统能够提供的「高可用」特性。
提升吞吐量。将一份数据复制多份并保存在多个副本节点上，还顺便带来一个好处：对于同一个数据对象的访问请求（至少是读请求）可以由多个副本节点分担，从而使得整个系统可以随着请求量的增加不断扩展。

一方面，复制带来了诸多好处；另一方面，它也带来了很多挑战，其中最重要的一个就是数据的一致性问题。由于同一份数据保存在了多个副本节点上，它们之间就存在数据不一致的风险。我们当然希望同一份数据的不同副本总是保持一致。换句话说，我们希望在其中一个副本上所做的修改，在其它副本上也能随时观察到（即读取到）。

当然我们心里都清楚，让所有副本在任何时刻都保持一致，是不可能的。因为副本之间的数据同步即使速度再快，也是需要时间的。不过幸运的是，我们其实并不关心所有时刻的数据一致性情况。只要系统能够保证，每当我们去「观察」的时候（即读取数据副本的时候），系统表现出来的行为是一致的，就可以了。换句话说，即使在两次「观察」之间，系统内部出现了短暂的数据不一致的情况，只要系统保证外部用户无论如何都发现不了，我们也是可以满意的。

这意味着，我们应该从系统用户（使用系统的开发者）的角度，来对数据一致性的要求进行定义。

实际上，早期的分布式系统设计者们对系统设计的要求，也是按照类似的思路进行的。在理想情况下，系统应该维持类似SSI (single-system image)[1]或distribution transparency[2]的特性。这两个概念要表达的核心意思是，系统内部有关分布式实现的复杂性应该对系统的外部用户透明；也就是说，对于系统的外部用户来说，系统应该表现得就好像只有一个单一的副本一样。如果系统能够提供这种「单一系统视图」或「透明性」，那么系统的使用者就能以比较简单的方式来使用系统；否则就可能带来很大的负担。

系统“表现得就好像只有一个单一的副本”，这是一个相当「笼统」的说法。在此我们讨论3个具体的例子：

我们先向一个副本节点写入x=42，然后读取数据对象x的值。显然，不管我们从哪个副本节点上进行读取，我们都希望读到最新写入的值（也就是42）。只有这样才合理。
两个系统用户分别在两个副本节点上同时执行写操作。其中，用户A在第1个副本上执行x=42；用户B在第2个副本上执行x=43。然后用户C读取x的值。虽然两个写操作是「同时」进行的，但为了让系统“表现得像只有一个副本”，我们还是需要对它们进行一个先后排序。又因为它们是「同时」执行的，所以谁先谁后都有可能是合理的。如果我们认为x=42在x=43之前先执行，那么读取到的x的值就应该是43；反过来，如果我们认为x=43在x=42之前先执行，那么读取到的x的值就应该是42。
用户A先在第1个副本上执行x=42，然后用户B再在第2个副本上执行x=43，最后用户C在第3个副本上读取x的值。仍然为了让系统“表现得像只有一个副本”，直觉上看，用户C读取到的x的值似乎应该是43。但是，也不一定非要如此。因为两个写操作是分别由用户A和用户B发起的，他们并不知道彼此谁先谁后（虽然从时间上看用户A的写操作确实在先）。所以，我们也可以选择认为用户B执行x=43在用户A执行x=42之前。这样的话，用户C读取到的x的值就应该是42。当然，根据本文后面的讨论，这种排序就不满足线性一致性了，但却满足顺序一致性。

从这些例子不难看出，一个系统在数据一致性上的具体表现如何，取决于系统对关键事件（读写操作）的排序和执行采取什么样的规则和限制。比如在上面第3个例子中，出现了两种对于读写操作的排序。前一种排序是：

用户A执行x=42。
用户B执行x=43。
用户C读取到x的值是43。

而第3个例子中的后一种排序是：

用户B执行x=43。
用户A执行x=42。
用户C读取到x的值是42。

虽然这两种排序结果不同，但它们都做到了让系统“表现得像只有一个副本”。它们的不同在于，前一种排序遵循了不同用户的操作的时间先后顺序，而后一种排序没有。实际上，如果我们要求系统满足线性一致性，就只能得到前一种排序结果；而如果只要求系统满足顺序一致性，就有可能得到后一种排序结果（等看完本文后面的讨论，你就能自己得到这些结论）。

可以这么说，一个分布式系统对于读写操作的某种排序和执行规则，就定义了一种一致性模型 (consistency model)。当一个系统选定了某种特定的一致性模型（比如线性一致性或顺序一致性），那么你就只能看到这种一致性模型所允许的那些操作序列。还是拿前面第3个例子来说明：如果你选定了线性一致性模型，那么系统就不会向你呈现后一种排序，你只能看到前一种排序。

另外，在前面的三个例子中，不管系统最终给出了哪种排序结果，所有系统的用户其实都对那种操作序列达成了一致的看法。还有一些一致性模型，并不要求所有用户对操作排序的结果达成唯一的一种看法。这样的一致性模型稍显复杂，我们会放在下一篇文章中再讨论（比如因果一致性）。

接下来，为了更清晰地认识一致性模型，我们来深入到线性一致性和顺序一致性的一些细节中去。

线性一致性和顺序一致性

在讨论之前，我们先把组成分布式系统的一些关键概念定义清楚：

整个系统可以看成由多个进程和一个共享的数据存储组成。对于数据存储的读写操作由进程发起。这里的进程，相当于本文前面提到的系统用户或系统使用者。
同一个进程发起的读写操作是先后顺序执行的。注意，这里的「进程」概念跟我们平常编程时用到的进程有所不同，进程里面不再分多个线程了。
数据存储可能有多个副本，但我们在讨论一致性模型的时候，把它看成一个整体来看待，不区分读写操作提交到了具体哪个副本上。
每个操作的执行，从开始调用到执行结束，都需要花一定的时间。因此，一个进程发起的操作还没有执行完的时候，另一个进程的操作可能就已经开始了。

可见，系统的多个进程是并发执行的。下面我们通过一个例子来说明这种并发执行的情况，进而解释顺序一致性的概念。

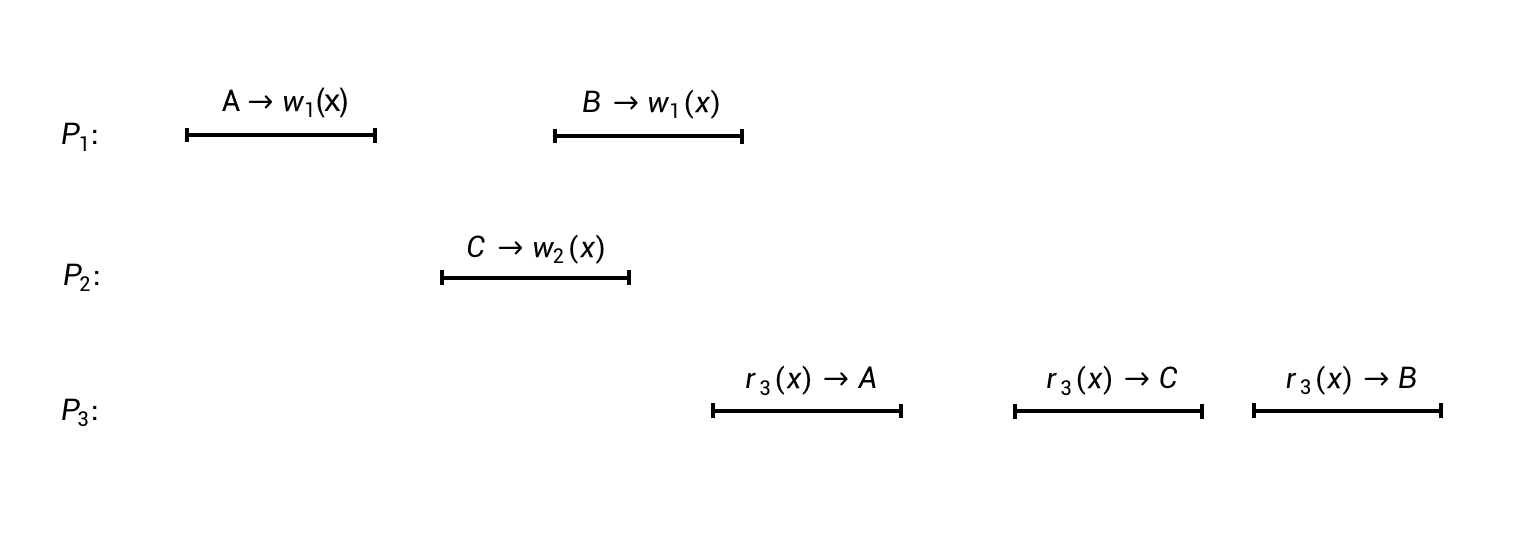
上面是一个类似「时空图」的图像，表达了3个进程（P₁、P₂和P₃）对于数据存储的读写执行过程。在这个图中，横向从左到右表示时间递增，黑色的线段表示每个操作的执行起止。线段上面的符号表示具体的读写操作：

A –> w_i(x)，表示一个写操作：第i个进程向数据对象x写入了值A。
r_i(x) –> A，表示一个读操作：第i个进程从数据对象x中读到了值A。

现在我们要考察的问题是：上图的这样一个执行过程，是否满足顺序一致性？要回答这个问题，我们首先得知道顺序一致性的定义是什么。

顺序一致性定义[3,4]：如果一个并发执行过程所包含的所有读写操作能够重排成一个全局线性有序的序列，并且这个序列满足以下两个条件，那么这个并发执行过程就是满足顺序一致性的：

条件I：重排后的序列中每一个读操作返回的值，必须等于前面对同一个数据对象的最近一次写操作所写入的值。
条件II：原来每个进程中各个操作的执行先后顺序，在这个重排后的序列中必须保持一致。

以上图的执行过程为例，我们重排所有的6个读写操作，可以得到如下的有序序列：

A –> w₁(x)
r₃(x) –> A
C –> w₂(x)
r₃(x) –> C
B –> w₁(x)
r₃(x) –> B

很容易看出，这个序列是满足前面顺序一致性定义中的两个条件的：

条件I：在这个重排后的序列中，每个读操作都返回了前面最近一次写入的值，比如第2个操作读到的值A，是前面第1个操作写入的；第4个操作读到的值C，是前面第3个操作写入的。
条件II：原来进程P₁中的两个写操作，A –> w₁(x)和B –> w₁(x)，在这个重排后的序列中仍然保持了先后顺序。与此类似，原来进程P₃中的3个读操作，在这个重排后的序列中也保持了原来的先后顺序。

所以现在我们可以回答前面的问题了：上图中的执行过程，是满足顺序一致性的。

你可能会问，顺序一致性为什么会这样定义呢？这个定义的初衷是什么？

我们可以试着这样理解：首先，重排成一个全局线性有序的序列，相当于系统对外表现出了一种「假象」，原本多进程并发执行的操作，好像是顺序执行的一样。本文前面提到过，理想情况下，分布式系统应该“表现得像只有一个副本”一样。顺序一致性正是遵循了这种「系统假象」，系统对外表现就好像在操作一个单一的副本，执行顺序也必然是可以看做顺序执行的。而条件I规定了系统的表现是合理的（即合乎逻辑的）；条件II则保证了以任何进程的视角来看，它所发起的操作执行顺序都是符合它原本的预期的。总之，一个满足顺序一致性的系统，对外表现就好像总是在操作一个副本一样。

我们再通过一个例子来看一看这个问题的反面——不满足顺序一致性的执行过程是怎样的。

这个图中的执行过程，与前面第一个图的执行过程非常相似，只是进程P₃的几个操作的执行顺序稍有变化。

我们根据前面顺序一致性的定义再来试着对这个执行过程中的所有操作进行重排：首先根据条件II和进程P₁的执行顺序，我们知道，A –> w₁(x)一定要排在B –> w₁(x)前面；再根据条件I，进程P₁的B –> w₁(x)一定要排在进程P₃的r₃(x) –> B前面。最后，再结合条件II和进程P₃的执行顺序，我们能够得出结论，进程P₁和进程P₃的所有操作，在最终重排后的完整序列中，必然保持以下的顺序：

A –> w₁(x)
B –> w₁(x)
r₃(x) –> B
r₃(x) –> C
r₃(x) –> A

我们会发现，上面的序列有两个地方不满足条件I：

第4个操作读到了值C，而前面最近一次写操作（第2个操作）所写入的值是B。
第5个操作读到了值A，而前面最近一次写操作（也是第2个操作）所写入的值是B。

我们还剩一个进程P₂的写操作，即C –> w₂(x)，没有放到最后这个序列中。也许我们可以试着将它放置到第3和第4个操作之间，这样就能把前面第一个不满足条件I的地方修复掉。但无论如何，也无法得到一个完全符合条件I和条件II的完整序列了。因此，前面第二个图中的执行过程，是不满足顺序一致性的。进一步说，如果一个系统的执行呈现出了这样的一种执行过程（如前面第二个图所示），那我们可以肯定地说，这个系统是没有遵守顺序一致性的。

我们再来考察一下线性一致性的概念。线性一致性的定义[5]，与顺序一致性非常相似，也是试图把所有读写操作重排成一个全局线性有序的序列，但除了满足前面的条件I和条件II之外，还要同时满足一个条件：

条件III：不同进程的操作，如果在时间上不重叠，那么它们的执行先后顺序，在这个重排后的序列中必须保持一致。

根据最新定义的条件III，我们来重新评判一下前面第一个图所展现出来的执行过程是不是满足它。为了阅读和讨论方便，我们把第一个图重新展示在下面：

针对条件III，我们分析一下各个操作之间的先后顺序：

进程P₁的B –> w₁(x)和进程P₂的C –> w₂(x)，在执行时间上是重叠的，所以它们的排序不受条件III的约束。即，在重排后的序列中，这两个操作谁先谁后都可以。同样，进程P₁的B –> w₁(x)和进程P₃的r₃(x) –> A，也是如此。
进程P₁的A –> w₁(x)和进程P₂的C –> w₂(x)，在执行时间上是不重叠的，即前一个操作都执行完了，后一个操作才开始执行。那么，这两个操作就必须满足条件III了：在重排后的序列中，A –> w₁(x)必须排在C –> w₂(x)前面。
与上面同样的道理，在重排后的序列中，进程P₂的C –> w₂(x)必须排在进程P₃的r₃(x) –> A之前。

容易看出，在遵守这样的先后关系约束的前提下，不管怎么重排，都无法得到一个满足条件I的完整序列了。所以说，前面第一个图所示的满足顺序一致性的执行过程，是不满足线性一致性的。

下面我们举一个满足线性一致性的例子：

上图的执行过程，所有操作重排后，可以得到如下的有序序列：

A –> w₁(x)
r₃(x) –> A
C –> w₂(x)
r₃(x) –> C
B –> w₁(x)
r₃(x) –> B

不难看出，这个序列是满足所有的条件I、条件II和条件III这三个条件的。因此，这个执行过程满足线性一致性。

细心的你可能已经发现了，最后这个线性一致性的例子，得到的重排后的序列，与开始第一个顺序一致性的例子重排后的序列，完全相同。当然，这两个例子中原始的多进程并发执行过程，是不同的。这是符合预期的（没有什么可奇怪的）。

现在我们可以仔细分析一下条件II和条件III，它们囊括了任意两个操作之间所有可能的先后关系：

进程内的任意两个操作之间，总是先后顺序执行的（执行时间上不可能重叠）；而根据条件II，它们的先后顺序在最后重排后的序列中也会保持。
不同进程的不同操作之间，在执行时间上可能重叠（并发执行），也可能不重叠。根据条件III，不重叠的两个操作，它们在时间上的先后顺序，在最后重排后的序列中会得以保持。而对于执行时间上重叠的两个操作，它们在最后重排后的序列中的先后顺序没有规定。

最后，我们比较一下顺序一致性和线性一致性：

它们都试图让系统“表现得像只有一个副本”一样。
它们都保证了程序执行顺序不会被打乱。体现在条件II对于进程内各个操作的排序保持上。
线性一致性考虑了时间先后顺序，而顺序一致性没有。
满足线性一致性的执行过程，肯定都满足顺序一致性；反之不一定。

注意一下上面第3点两者在时间先后顺序上的不同。这意味着：

线性一致性隐含了时效性保证（recency guarantee）。它保证我们总是能读到数据最新的值。
在顺序一致性中，我们有可能读到旧版本的数据。比如，在本文第一个顺序一致性的例子中，在进程P₂将数据对象x的值写成了C之后，进程P₃仍然读到了旧的值（A）。

最终一致性和它的特殊性

我们在上一篇文章中提到过，CAP定理[6]中的C，指的就是线性一致性 (linearizability)。它也经常被称为「强一致性」。

根据CAP定理，当存在网络分区的时候，我们必须在可用性 (availability) 和强一致性之间进行取舍。

另外，即使在没有网络分区存在的情况下，我们也必须在延迟 (latency) 和强一致性之间进行取舍[7]。这是因为，系统维持强一致性是有成本的。想要维持越强的一致性，就需要在副本节点之间做更多的通信和协调工作，因此会增加操作的总延迟，进而降低整个系统的性能。

从20世纪90年代中期开始，互联网开始蓬勃发展，系统的规模也变得越来越大。人们设计大型分布式系统的指导思想，也逐步开始更倾向于系统的高可用性和高性能。取舍的结果就是，降低系统提供的一致性保障。这其中非常重要的一条思路就是最终一致性[2]。

最终一致性的设计思路，不再试图提供单一系统视图 (SSI)，即不再试图让系统“表现得像只有一个副本”一样。它允许读到旧版本的数据。最终一致性的原始出处是论文[2]，作者在论文中给出的最终一致性的定义如下：

Eventual consistency. This is a specific form of weak consistency; the storage system guarantees that if no new updates are made to the object, eventually all accesses will return the last updated value.
(译文：最终一致性是弱一致性的一种特殊形式；存储系统保证，如果对象没有新的修改操作，那么所有的访问最终都会返回最新写入的值。)

我们发现，虽然最终一致性和本文前面讨论的线性一致性或顺序一致性在命名上非常相似，但它的定义却与后两者存在非常大的差别。深层的原因在于，它们其实属于不同类别的系统属性 (property)。线性一致性和顺序一致性属于safety property（安全性）；而最终一致性属于liveness property（活性）[8]。

一个并发程序或者一个分布式系统，它们的执行所展现出来的系统属性，可以分为两大类：

safety：它表示「坏事」永远不会发生。比如，一个系统如果遵守线性一致性或顺序一致性，那么就永远不会出现违反三个（对于顺序一致性来说是两个）条件的执行过程。而一旦系统出现问题，safety被违反了，我们也能明确指出是在哪个时间点上出现意外的。
liveness：它表示「好事」最终会发生。这种属性听起来会比较神奇：在任何一个时间点，你都无法判定liveness被违反了。因为，即使你期望的「好事」还没有发生，也不代表它未来不会发生。就像最终一致性一样，即使当前系统处于不一致的状态，也不代表未来系统就不会达到一致的状态。而只要系统存在“在未来某个时刻达到一致状态”的可能性，最终一致性就没有被违反。另外，可用性 (availability) 也属于liveness属性。

由此可见，我们在前一小节之所以能够将线性一致性和顺序一致性放在一起讨论和比较，是因为它们都属于safety属性。而最终一致性属于liveness属性，跟这两者存在本质的区别。实际上，最终一致性有点名不副实，它更好的名字可能是收敛性 (convergence)，表示所有副本最终都会收敛到相同的值[9]。

通常来说，只有当safety和liveness这两种属性被同时考虑时，一个系统才能提供有意义的系统保证[1]。而当系统设计者遵循最终一致性的设计思路时，相当于放弃了所有的safety属性。这意味着，对于系统使用者来说，你必须针对数据不一致的可能性做好补偿措施 (compensation)。这也是最终一致性系统难用的地方。但不管怎么说，最终一致性仍然被认为是系统提供数据一致性的最低要求[1]。

一致性的强弱关系

在本文开头，我们提到过，通常人们把线性一致性称为「强一致性」，把最终一致性称为「弱一致性」。但对于指代特定的一种一致性模型来说，「强一致性」和「弱一致性」都不是一个好名字。因为强和弱，是个相对的概念。

根据本文前面的讨论，从线性一致性，到顺序一致性，再到最终一致性，一致性的强度依次减弱。但是，一致性模型的强弱关系，其实是有更严格的定义的：

当且仅当一个一致性模型所能接受的执行过程，都能被另一个一致性模型所接受时（前者的集合是后者集合的子集），我们就说前者是比后者「更强」(stronger) 的一致性模型。

按照这个更严格的强弱关系定义，线性一致性是比顺序一致性更强的一致性模型。这是因为，线性一致性比顺序一致性多了一个条件III，所以凡是满足线性一致性的执行过程，肯定也满足顺序一致性。

我们仔细分析一下也能知道，一致性模型的强弱关系定义，是基于safety属性定义的。所以，将线性一致性或顺序一致性与最终一致性比较强弱，这并不是一个严格的做法。实际上，就像我们前一小节所讨论的，最终一致性在safety方面提供的保证为零，它是属于liveness的概念。一个系统可以在提供最终一致性的同时，也提供另外一种更强一点的带有safety属性的一致性（比如因果一致性）。

小结

就如同我在之前另外一篇文章《漫谈分布式系统、拜占庭将军问题与区块链》中所指出的，理解问题本身比知道问题的答案要重要的多。本文中，我们辨析了线性一致性、顺序一致性、最终一致性这些概念，以及他们的关系和区别。由此我们了解到了分布式系统的一些核心问题，但我们并未讨论怎么解决这些问题。比如，采用什么算法才能提供线性一致性；面对最终一致性的系统，应该怎样编程，包括怎样处理边界情况，等等。相对于理解问题本身而言，这些反而都是细节。

在这个系列的下一篇文章中，我们将依然遵循这样的思路，具体解析因果一致性，以及分布式系统更深层的事件排序问题。

（正文完）

参考文献：

[1] Peter Bailis, Ali Ghodsi, “Eventual Consistency Today: Limitations, Extensions, and Beyond”, 2013.
[2] Werner Vogels, “Eventually Consistent”, 2008.
[3] Leslie Lamport, “How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Progranm”, 1979.
[4] Mustaque Ahamad, Gil Neiger, James E. Burns, et al, “Causal Memory: Definitions, Implementation and Programming”, 1994.
[5] Maurice P. Herlihy, Jeannette M. Wing, “Linearizability: A Correctness Condition for Concurrent Objects”, 1990.
[6] Seth Gilbert, Nancy Lynch, “Brewer’s Conjecture and the Feasibility of Consistent, Available, Partition-Tolerant Web”, 2002.
[7] Peter Bailis, Ali Ghodsi, et al, “Bolt-on Causal Consistency”, 2013.
[8] Bowen Alpern, Fred B. Schneider, “Defining Liveness”, 1985.
[9] Martin Kleppmann,《Designing Data-Intensive Applications》, 2017.
[10] Prince Mahajan, Lorenzo Alvisi, Mike Dahlin, “Consistency, Availability, and Convergence”, 2011.

其它精选文章：

原创文章，转载请注明出处，并包含下面的二维码！否则拒绝转载！
本文链接：http://zhangtielei.com/posts/blog-distributed-strong-weak-consistency.html
欢迎关注我的个人微博：微博上搜索我的名字「张铁蕾」。

上篇：条分缕析分布式：到底什么是一致性？

下篇：条分缕析分布式：因果一致性和相对论时空