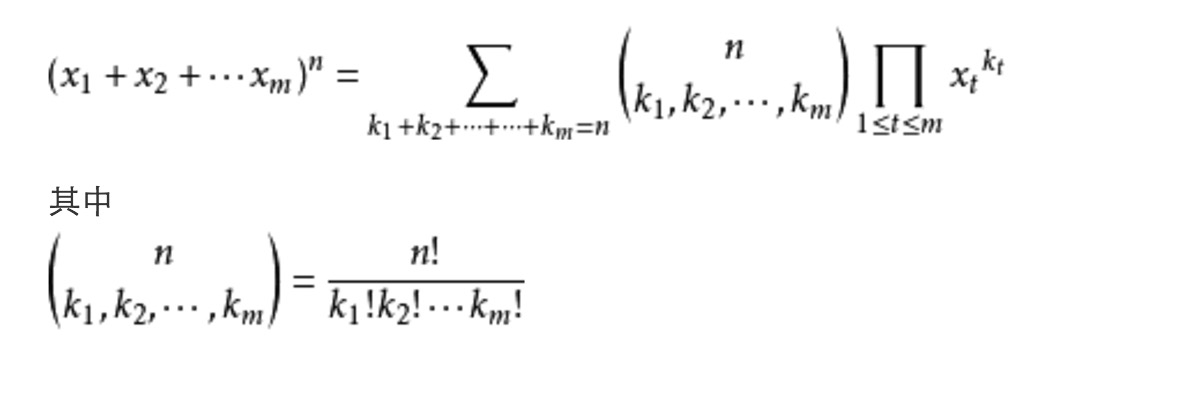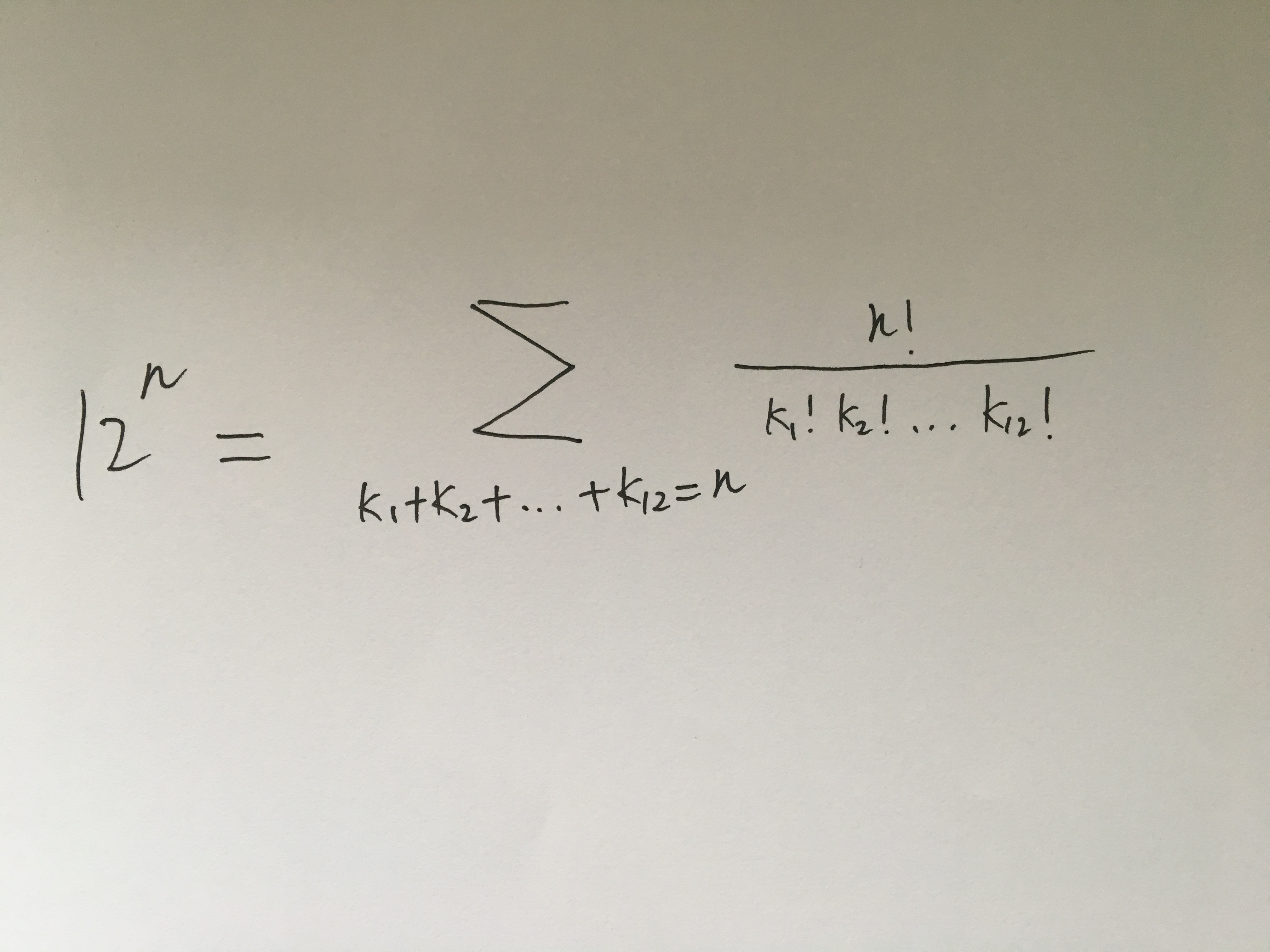光棍节发生的故事:生日谜题
2016-11-13
今天周末,给大家讲个小故事。
微爱公司有一项传统:每个月要选择一天,给当月所有过生日的同学一起庆祝生日。一般来说,当月有几个过生日的同学,公司行政就准备几个蛋糕。
今年11月份的生日庆祝,就选择在了光棍节(11月11号)下午。结果大家发现,这个月竟然只有一位同学过生日。这大概是一个小概率事件,但概率到底是多少呢?于是,Vito(CEO)突发奇想,给大家出了一道概率题,答对的同学呢,有4位数以上的奖金哦。
题目是这样的:计算一年内只有一个月里面仅有一位同学过生日的概率。
补充说明:因为要求一年内“只有一个月”,所以如果有两个月都仅有一位同学过生日,这种情况是不算的。另外,为了简化问题,不考虑每个月天数不同的情况,都认为30天即可。
于是,生日庆祝会结束之后,整个公司的同学,包括前台的小妹,都展开了计算。
很快,QQ群里就出现了一打以上的公式和结果。但可惜的是,它们都各不相同!我也顺手写了个公式,但随即就发现是有问题的,有些情况被重复计算了。
同学们之间发生了激烈的争论。计算和讨论一直持续到下班之后。奖金也因此暂时没有人领走。
读者们看到这里,可以暂停五分钟,想想看有没有合适的方法或公式。
分析
大家都试图列出一个简单的公式来表达这个概率,包含加减乘除以及指数运算。运用的数学方法,就是概率论里的排列组合的相关知识。
但是,真正准确的结果到底能不能归结到一个足够简洁的公式上呢?让我们分析一下。
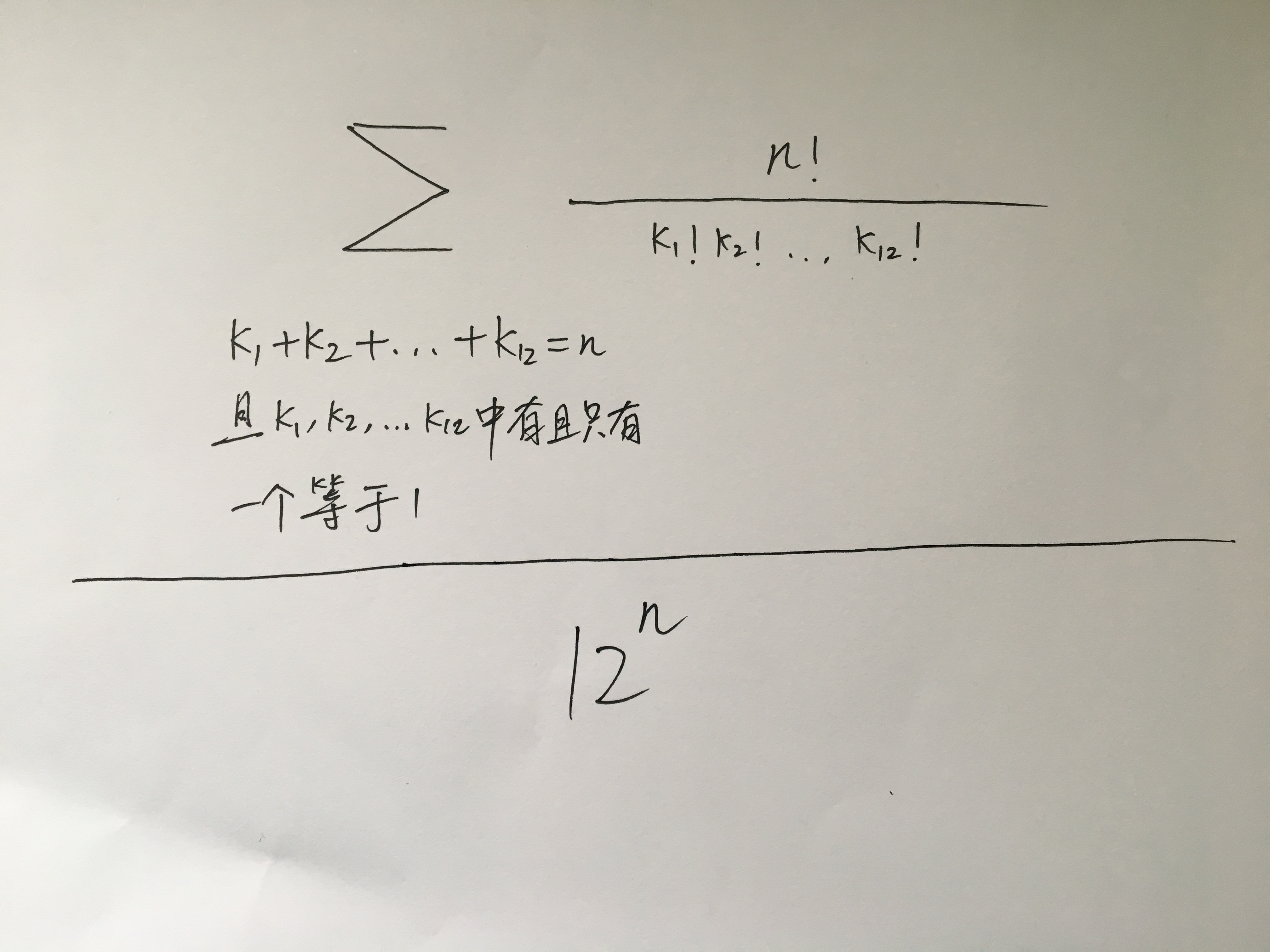
设公司总人数为n,那么总共可能的生日排列情况的个数为12n。
问题相当于在总共12n个排列情况中选出符合条件的那些项。仔细思考的话,这个问题的本质其实是在一个多项式定理(二项式定理的推广形式)的展开项中找出符合预期条件的那些项,然后对这些项求和。
多项式定理是这样的:
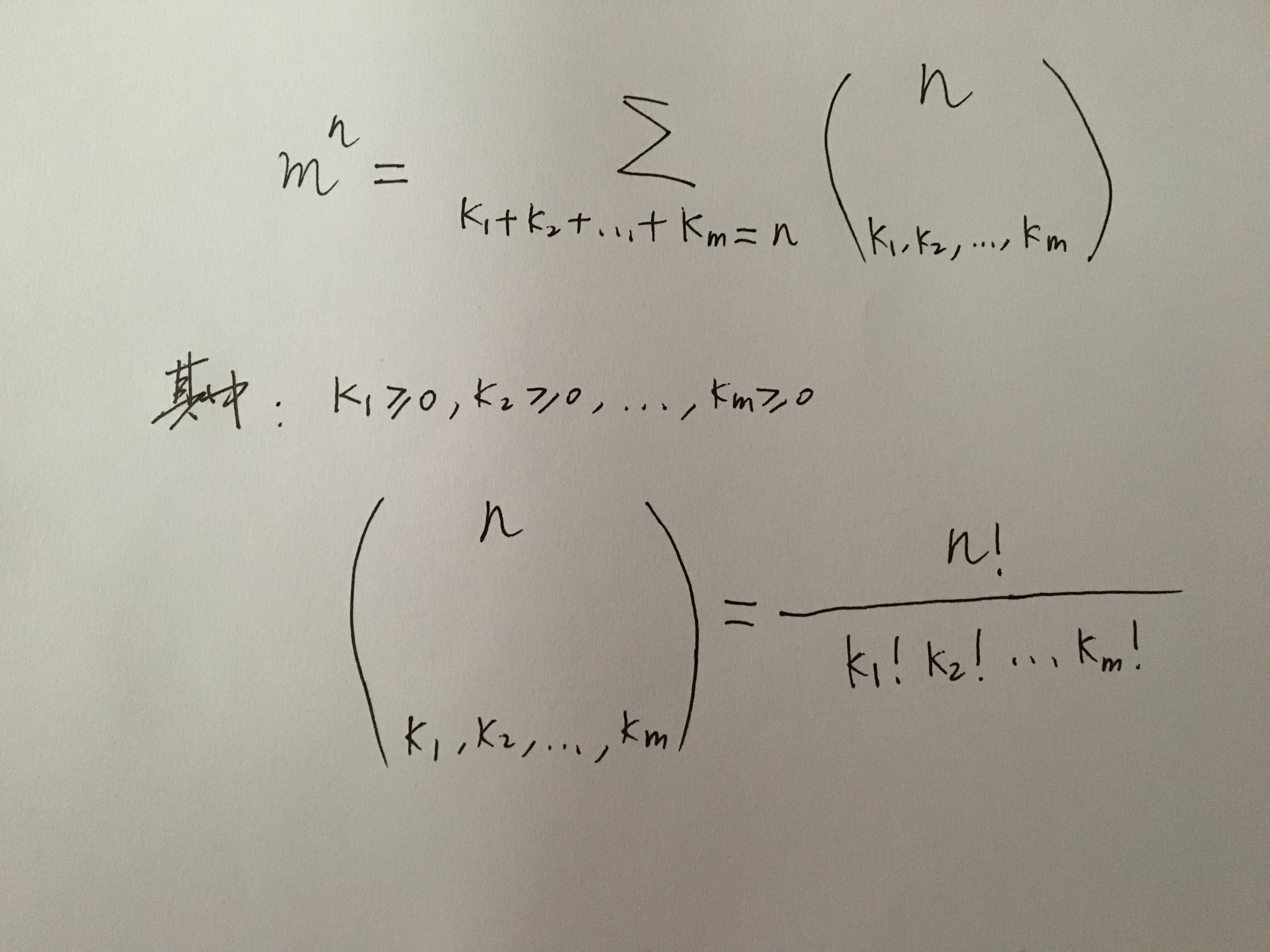
令x1=x2=…=xm=1,得到多项式定理的一个特殊形式:
令m=12,就得到了对于12n的展开式:
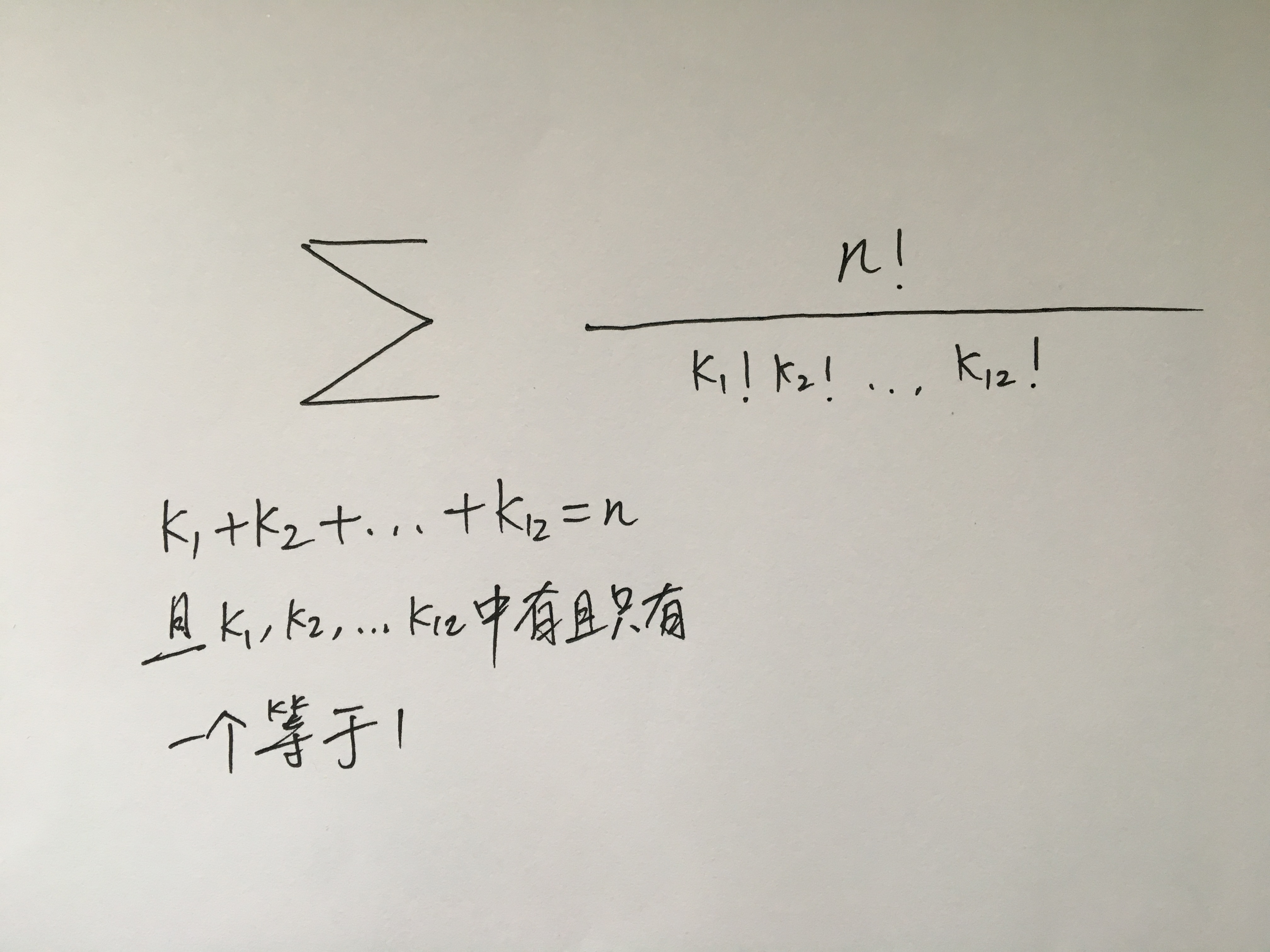
而这其中符合条件“只有一个月里面仅有一位同学过生日”的所有项,相当于:
因此,我们最终要计算的概率,它的精确的数学形式是:
能否写出一个更简单的公式,取决于能否把上面这个式子化简。
在平常的概率考试中,如果出现类似这种排列组合的题目,那么这个题目的条件肯定是被“精心策划”过的,使得需要的展开项或者能够重新组合成多项式定理的形式(能重新合并成指数形式),或者涉及到的数字较小能够很容易的穷举。只有这样,才能保证题目能够让一个至少具有中学生水平的答题者在限定的考试时间内算出结果。但我们这里的这个问题,是一个更“实际的问题”,或者说题目条件是“随意挑选”的。在这个条件下,上面的公式似乎很难再进一步简化。
之前大家在QQ群里列出的看似简单的公式,应该都存在重复或者遗漏的情况。
但是,即使上面最后的那个公式无法再化简了,我们仍然能进行计算。不过必须借助编程的手段了。最简单的实现就是编写一个递归的方法来计数。
即使借助编程的手段,这个公式仍然不好计算。计算它有两个难点:(1)中间数据太大,基本属于是天文级数据,不能使用64位的整型来计算(一般语言的整型最大也就只能表示64位)。计算的话,需要使用一个能计算超长位数的编程环境。(2)需要对一个很大的问题空间进行搜索,虽然已经比指数要小很多,但复杂度仍然很高。而如果按原问题暴力搜索12n这么大的空间,则问题规模更大。
对于人数n比较小的情况,还是比较容易计算的。下面给出几个结果:
- n=12,概率为0.023169
- n=13,概率为0.024052
- n=14,概率为0.025208
- n=15,概率为0.027055
- n=16,概率为0.029525
- n=17,概率为0.032689
- n=18,概率为0.036636
- n=19,概率为0.041469
- n=20,概率为0.047306
看起来,人数越多,概率越大,但其实这个增势不会一直持续下去。人数足够多的时候,更可能发生的情况是一个月内有超过2个人过生日了。所以,随着n的增大,这个概率最终会越来越小。
如果你有兴趣计算上面这个公式的话,欢迎给我留言讨论^-^
(完)
其它精选文章:
- 小白的数据进阶之路(上)
- Redis内部数据结构详解(6)——skiplist
- 你需要了解深度学习和神经网络这项技术吗?
- 论人生之转折
- 技术的正宗与野路子
- 程序员的那些反模式
- 程序员的宇宙时间线
- Android端外推送到底有多烦?
- Android和iOS开发中的异步处理(四)——异步任务和队列
- 用树型模型管理App数字和红点提示
原创文章,转载请注明出处,并包含下面的二维码!否则拒绝转载!
本文链接:http://zhangtielei.com/posts/blog-anniversary-puzzle.html
欢迎关注我的个人微博:微博上搜索我的名字「张铁蕾」。