Redis内部数据结构详解(1)——dict
2016-05-31
如果你使用过Redis,一定会像我一样对它的内部实现产生兴趣。《Redis内部数据结构详解》是我准备写的一个系列,也是我个人对于之前研究Redis的一个阶段性总结,着重讲解Redis在内存中的数据结构实现(暂不涉及持久化的话题)。Redis本质上是一个数据结构服务器(data structures server),以高效的方式实现了多种现成的数据结构,研究它的数据结构和基于其上的算法,对于我们自己提升局部算法的编程水平有很重要的参考意义。
当我们在本文中提到Redis的“数据结构”,可能是在两个不同的层面来讨论它。
第一个层面,是从使用者的角度。比如:
- string
- list
- hash
- set
- sorted set
这一层面也是Redis暴露给外部的调用接口。
第二个层面,是从内部实现的角度,属于更底层的实现。比如:
- dict
- sds
- ziplist
- quicklist
- skiplist
第一个层面的“数据结构”,Redis的官方文档(http://redis.io/topics/data-types-intro)有详细的介绍。本文的重点在于讨论第二个层面,Redis数据结构的内部实现,以及这两个层面的数据结构之间的关系:Redis如何通过组合第二个层面的各种基础数据结构来实现第一个层面的更高层的数据结构。
在讨论任何一个系统的内部实现的时候,我们都要先明确它的设计原则,这样我们才能更深刻地理解它为什么会进行如此设计的真正意图。在本文接下来的讨论中,我们主要关注以下几点:
- 存储效率(memory efficiency)。Redis是专用于存储数据的,它对于计算机资源的主要消耗就在于内存,因此节省内存是它非常非常重要的一个方面。这意味着Redis一定是非常精细地考虑了压缩数据、减少内存碎片等问题。
- 快速响应时间(fast response time)。与快速响应时间相对的,是高吞吐量(high throughput)。Redis是用于提供在线访问的,对于单个请求的响应时间要求很高,因此,快速响应时间是比高吞吐量更重要的目标。有时候,这两个目标是矛盾的。
- 单线程(single-threaded)。Redis的性能瓶颈不在于CPU资源,而在于内存访问和网络IO。而采用单线程的设计带来的好处是,极大简化了数据结构和算法的实现。相反,Redis通过异步IO和pipelining等机制来实现高速的并发访问。显然,单线程的设计,对于单个请求的快速响应时间也提出了更高的要求。
本文是《Redis内部数据结构详解》系列的第一篇,讲述Redis一个重要的基础数据结构:dict。
dict是一个用于维护key和value映射关系的数据结构,与很多语言中的Map或dictionary类似。Redis的一个database中所有key到value的映射,就是使用一个dict来维护的。不过,这只是它在Redis中的一个用途而已,它在Redis中被使用的地方还有很多。比如,一个Redis hash结构,当它的field较多时,便会采用dict来存储。再比如,Redis配合使用dict和skiplist来共同维护一个sorted set。这些细节我们后面再讨论,在本文中,我们集中精力讨论dict本身的实现。
dict本质上是为了解决算法中的查找问题(Searching),一般查找问题的解法分为两个大类:一个是基于各种平衡树,一个是基于哈希表。我们平常使用的各种Map或dictionary,大都是基于哈希表实现的。在不要求数据有序存储,且能保持较低的哈希值冲突概率的前提下,基于哈希表的查找性能能做到非常高效,接近O(1),而且实现简单。
在Redis中,dict也是一个基于哈希表的算法。和传统的哈希算法类似,它采用某个哈希函数从key计算得到在哈希表中的位置,采用拉链法解决冲突,并在装载因子(load factor)超过预定值时自动扩展内存,引发重哈希(rehashing)。Redis的dict实现最显著的一个特点,就在于它的重哈希。它采用了一种称为增量式重哈希(incremental rehashing)的方法,在需要扩展内存时避免一次性对所有key进行重哈希,而是将重哈希操作分散到对于dict的各个增删改查的操作中去。这种方法能做到每次只对一小部分key进行重哈希,而每次重哈希之间不影响dict的操作。dict之所以这样设计,是为了避免重哈希期间单个请求的响应时间剧烈增加,这与前面提到的“快速响应时间”的设计原则是相符的。
下面进行详细介绍。
dict的数据结构定义
为了实现增量式重哈希(incremental rehashing),dict的数据结构里包含两个哈希表。在重哈希期间,数据从第一个哈希表向第二个哈希表迁移。
dict的C代码定义如下(出自Redis源码dict.h):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
typedef struct dictEntry {
void *key;
union {
void *val;
uint64_t u64;
int64_t s64;
double d;
} v;
struct dictEntry *next;
} dictEntry;
typedef struct dictType {
unsigned int (*hashFunction)(const void *key);
void *(*keyDup)(void *privdata, const void *key);
void *(*valDup)(void *privdata, const void *obj);
int (*keyCompare)(void *privdata, const void *key1, const void *key2);
void (*keyDestructor)(void *privdata, void *key);
void (*valDestructor)(void *privdata, void *obj);
} dictType;
/* This is our hash table structure. Every dictionary has two of this as we
* implement incremental rehashing, for the old to the new table. */
typedef struct dictht {
dictEntry **table;
unsigned long size;
unsigned long sizemask;
unsigned long used;
} dictht;
typedef struct dict {
dictType *type;
void *privdata;
dictht ht[2];
long rehashidx; /* rehashing not in progress if rehashidx == -1 */
int iterators; /* number of iterators currently running */
} dict;
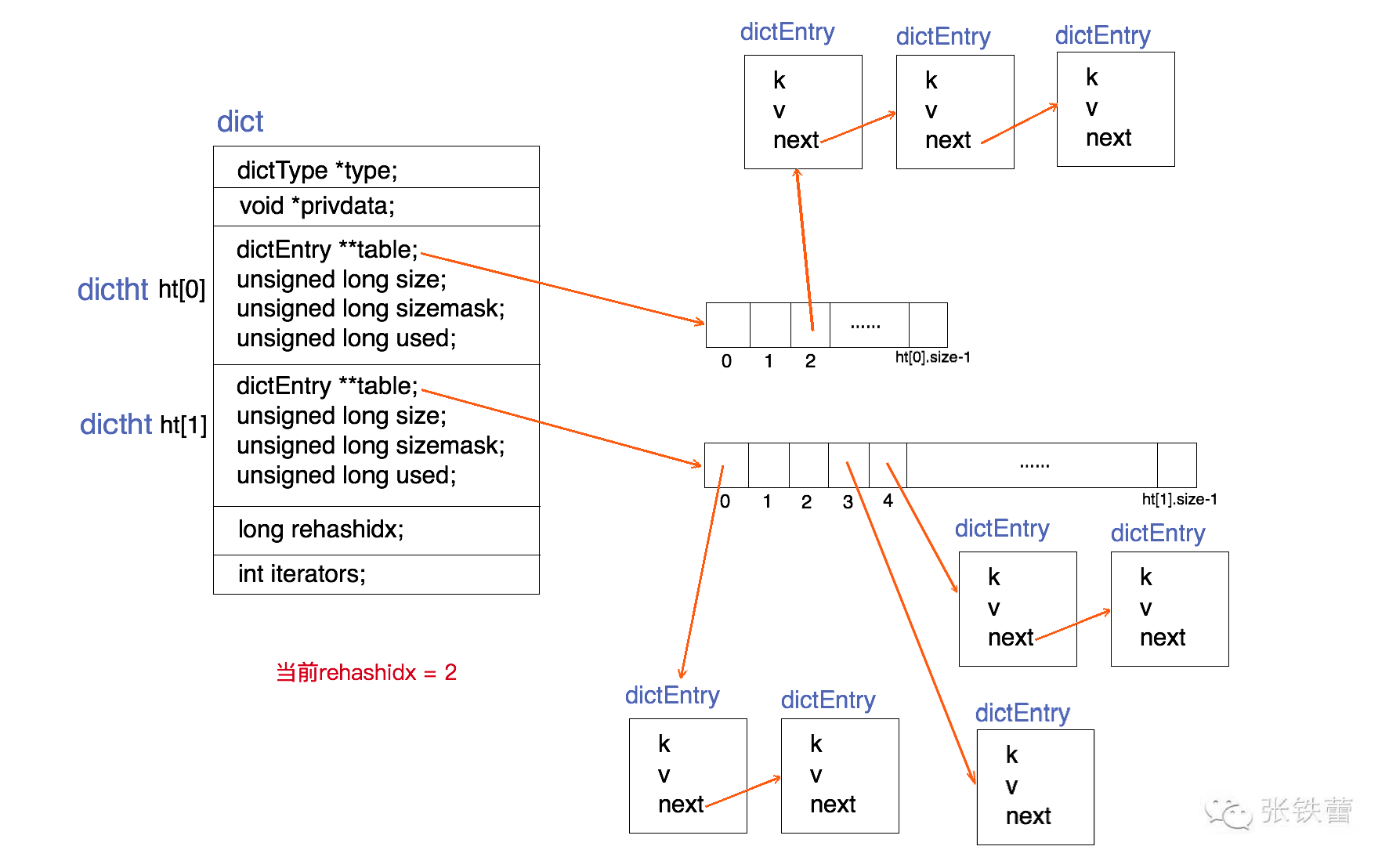
为了能更清楚地展示dict的数据结构定义,我们用一张结构图来表示它。如下。
结合上面的代码和结构图,可以很清楚地看出dict的结构。一个dict由如下若干项组成:
- 一个指向dictType结构的指针(type)。它通过自定义的方式使得dict的key和value能够存储任何类型的数据。
- 一个私有数据指针(privdata)。由调用者在创建dict的时候传进来。
- 两个哈希表(ht[2])。只有在重哈希的过程中,ht[0]和ht[1]才都有效。而在平常情况下,只有ht[0]有效,ht[1]里面没有任何数据。上图表示的就是重哈希进行到中间某一步时的情况。
- 当前重哈希索引(rehashidx)。如果rehashidx = -1,表示当前没有在重哈希过程中;否则,表示当前正在进行重哈希,且它的值记录了当前重哈希进行到哪一步了。
- 当前正在进行遍历的iterator的个数。这不是我们现在讨论的重点,暂时忽略。
dictType结构包含若干函数指针,用于dict的调用者对涉及key和value的各种操作进行自定义。这些操作包含:
- hashFunction,对key进行哈希值计算的哈希算法。
- keyDup和valDup,分别定义key和value的拷贝函数,用于在需要的时候对key和value进行深拷贝,而不仅仅是传递对象指针。
- keyCompare,定义两个key的比较操作,在根据key进行查找时会用到。
- keyDestructor和valDestructor,分别定义对key和value的析构函数。
私有数据指针(privdata)就是在dictType的某些操作被调用时会传回给调用者。
需要详细察看的是dictht结构。它定义一个哈希表的结构,由如下若干项组成:
- 一个dictEntry指针数组(table)。key的哈希值最终映射到这个数组的某个位置上(对应一个bucket)。如果多个key映射到同一个位置,就发生了冲突,那么就拉出一个dictEntry链表。
- size:标识dictEntry指针数组的长度。它总是2的指数。
- sizemask:用于将哈希值映射到table的位置索引。它的值等于(size-1),比如7, 15, 31, 63,等等,也就是用二进制表示的各个bit全1的数字。每个key先经过hashFunction计算得到一个哈希值,然后计算(哈希值 & sizemask)得到在table上的位置。相当于计算取余(哈希值 % size)。
- used:记录dict中现有的数据个数。它与size的比值就是装载因子(load factor)。这个比值越大,哈希值冲突概率越高。
dictEntry结构中包含k, v和指向链表下一项的next指针。k是void指针,这意味着它可以指向任何类型。v是个union,当它的值是uint64_t、int64_t或double类型时,就不再需要额外的存储,这有利于减少内存碎片。当然,v也可以是void指针,以便能存储任何类型的数据。
dict的创建(dictCreate)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
dict *dictCreate(dictType *type,
void *privDataPtr)
{
dict *d = zmalloc(sizeof(*d));
_dictInit(d,type,privDataPtr);
return d;
}
int _dictInit(dict *d, dictType *type,
void *privDataPtr)
{
_dictReset(&d->ht[0]);
_dictReset(&d->ht[1]);
d->type = type;
d->privdata = privDataPtr;
d->rehashidx = -1;
d->iterators = 0;
return DICT_OK;
}
static void _dictReset(dictht *ht)
{
ht->table = NULL;
ht->size = 0;
ht->sizemask = 0;
ht->used = 0;
}
dictCreate为dict的数据结构分配空间并为各个变量赋初值。其中两个哈希表ht[0]和ht[1]起始都没有分配空间,table指针都赋为NULL。这意味着要等第一个数据插入时才会真正分配空间。
dict的查找(dictFind)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#define dictIsRehashing(d) ((d)->rehashidx != -1)
dictEntry *dictFind(dict *d, const void *key)
{
dictEntry *he;
unsigned int h, idx, table;
if (d->ht[0].used + d->ht[1].used == 0) return NULL; /* dict is empty */
if (dictIsRehashing(d)) _dictRehashStep(d);
h = dictHashKey(d, key);
for (table = 0; table <= 1; table++) {
idx = h & d->ht[table].sizemask;
he = d->ht[table].table[idx];
while(he) {
if (key==he->key || dictCompareKeys(d, key, he->key))
return he;
he = he->next;
}
if (!dictIsRehashing(d)) return NULL;
}
return NULL;
}
上述dictFind的源码,根据dict当前是否正在重哈希,依次做了这么几件事:
- 如果当前正在进行重哈希,那么将重哈希过程向前推进一步(即调用_dictRehashStep)。实际上,除了查找,插入和删除也都会触发这一动作。这就将重哈希过程分散到各个查找、插入和删除操作中去了,而不是集中在某一个操作中一次性做完。
- 计算key的哈希值(调用dictHashKey,里面的实现会调用前面提到的hashFunction)。
- 先在第一个哈希表ht[0]上进行查找。在table数组上定位到哈希值对应的位置(如前所述,通过哈希值与sizemask进行按位与),然后在对应的dictEntry链表上进行查找。查找的时候需要对key进行比较,这时候调用dictCompareKeys,它里面的实现会调用到前面提到的keyCompare。如果找到就返回该项。否则,进行下一步。
- 判断当前是否在重哈希,如果没有,那么在ht[0]上的查找结果就是最终结果(没找到,返回NULL)。否则,在ht[1]上进行查找(过程与上一步相同)。
下面我们有必要看一下增量式重哈希的_dictRehashStep的实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
static void _dictRehashStep(dict *d) {
if (d->iterators == 0) dictRehash(d,1);
}
int dictRehash(dict *d, int n) {
int empty_visits = n*10; /* Max number of empty buckets to visit. */
if (!dictIsRehashing(d)) return 0;
while(n-- && d->ht[0].used != 0) {
dictEntry *de, *nextde;
/* Note that rehashidx can't overflow as we are sure there are more
* elements because ht[0].used != 0 */
assert(d->ht[0].size > (unsigned long)d->rehashidx);
while(d->ht[0].table[d->rehashidx] == NULL) {
d->rehashidx++;
if (--empty_visits == 0) return 1;
}
de = d->ht[0].table[d->rehashidx];
/* Move all the keys in this bucket from the old to the new hash HT */
while(de) {
unsigned int h;
nextde = de->next;
/* Get the index in the new hash table */
h = dictHashKey(d, de->key) & d->ht[1].sizemask;
de->next = d->ht[1].table[h];
d->ht[1].table[h] = de;
d->ht[0].used--;
d->ht[1].used++;
de = nextde;
}
d->ht[0].table[d->rehashidx] = NULL;
d->rehashidx++;
}
/* Check if we already rehashed the whole table... */
if (d->ht[0].used == 0) {
zfree(d->ht[0].table);
d->ht[0] = d->ht[1];
_dictReset(&d->ht[1]);
d->rehashidx = -1;
return 0;
}
/* More to rehash... */
return 1;
}
dictRehash每次将重哈希至少向前推进n步(除非不到n步整个重哈希就结束了),每一步都将ht[0]上某一个bucket(即一个dictEntry链表)上的每一个dictEntry移动到ht[1]上,它在ht[1]上的新位置根据ht[1]的sizemask进行重新计算。rehashidx记录了当前尚未迁移(有待迁移)的ht[0]的bucket位置。
如果dictRehash被调用的时候,rehashidx指向的bucket里一个dictEntry也没有,那么它就没有可迁移的数据。这时它尝试在ht[0].table数组中不断向后遍历,直到找到下一个存有数据的bucket位置。如果一直找不到,则最多走n*10步,本次重哈希暂告结束。
最后,如果ht[0]上的数据都迁移到ht[1]上了(即d->ht[0].used == 0),那么整个重哈希结束,ht[0]变成ht[1]的内容,而ht[1]重置为空。
根据以上对于重哈希过程的分析,我们容易看出,本文前面的dict结构图中所展示的正是rehashidx=2时的情况,前面两个bucket(ht[0].table[0]和ht[0].table[1])都已经迁移到ht[1]上去了。
dict的插入(dictAdd和dictReplace)
dictAdd插入新的一对key和value,如果key已经存在,则插入失败。
dictReplace也是插入一对key和value,不过在key存在的时候,它会更新value。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
int dictAdd(dict *d, void *key, void *val)
{
dictEntry *entry = dictAddRaw(d,key);
if (!entry) return DICT_ERR;
dictSetVal(d, entry, val);
return DICT_OK;
}
dictEntry *dictAddRaw(dict *d, void *key)
{
int index;
dictEntry *entry;
dictht *ht;
if (dictIsRehashing(d)) _dictRehashStep(d);
/* Get the index of the new element, or -1 if
* the element already exists. */
if ((index = _dictKeyIndex(d, key)) == -1)
return NULL;
/* Allocate the memory and store the new entry.
* Insert the element in top, with the assumption that in a database
* system it is more likely that recently added entries are accessed
* more frequently. */
ht = dictIsRehashing(d) ? &d->ht[1] : &d->ht[0];
entry = zmalloc(sizeof(*entry));
entry->next = ht->table[index];
ht->table[index] = entry;
ht->used++;
/* Set the hash entry fields. */
dictSetKey(d, entry, key);
return entry;
}
static int _dictKeyIndex(dict *d, const void *key)
{
unsigned int h, idx, table;
dictEntry *he;
/* Expand the hash table if needed */
if (_dictExpandIfNeeded(d) == DICT_ERR)
return -1;
/* Compute the key hash value */
h = dictHashKey(d, key);
for (table = 0; table <= 1; table++) {
idx = h & d->ht[table].sizemask;
/* Search if this slot does not already contain the given key */
he = d->ht[table].table[idx];
while(he) {
if (key==he->key || dictCompareKeys(d, key, he->key))
return -1;
he = he->next;
}
if (!dictIsRehashing(d)) break;
}
return idx;
}
以上是dictAdd的关键实现代码。我们主要需要注意以下几点:
- 它也会触发推进一步重哈希(_dictRehashStep)。
- 如果正在重哈希中,它会把数据插入到ht[1];否则插入到ht[0]。
- 在对应的bucket中插入数据的时候,总是插入到dictEntry的头部。因为新数据接下来被访问的概率可能比较高,这样再次查找它时就比较次数较少。
- _dictKeyIndex在dict中寻找插入位置。如果不在重哈希过程中,它只查找ht[0];否则查找ht[0]和ht[1]。
- _dictKeyIndex可能触发dict内存扩展(_dictExpandIfNeeded,它将哈希表长度扩展为原来两倍,具体请参考dict.c中源码)。
dictReplace在dictAdd基础上实现,如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int dictReplace(dict *d, void *key, void *val)
{
dictEntry *entry, auxentry;
/* Try to add the element. If the key
* does not exists dictAdd will suceed. */
if (dictAdd(d, key, val) == DICT_OK)
return 1;
/* It already exists, get the entry */
entry = dictFind(d, key);
/* Set the new value and free the old one. Note that it is important
* to do that in this order, as the value may just be exactly the same
* as the previous one. In this context, think to reference counting,
* you want to increment (set), and then decrement (free), and not the
* reverse. */
auxentry = *entry;
dictSetVal(d, entry, val);
dictFreeVal(d, &auxentry);
return 0;
}
在key已经存在的情况下,dictReplace会同时调用dictAdd和dictFind,这其实相当于两次查找过程。这里Redis的代码不够优化。
dict的删除(dictDelete)
dictDelete的源码这里忽略,具体请参考dict.c。需要稍加注意的是:
- dictDelete也会触发推进一步重哈希(_dictRehashStep)
- 如果当前不在重哈希过程中,它只在ht[0]中查找要删除的key;否则ht[0]和ht[1]它都要查找。
- 删除成功后会调用key和value的析构函数(keyDestructor和valDestructor)。
dict的实现相对来说比较简单,本文就介绍到这。在下一篇中我们将会介绍Redis中动态字符串的实现——sds,敬请期待。
原创文章,转载请注明出处,并包含下面的二维码!否则拒绝转载!
本文链接:http://zhangtielei.com/posts/blog-redis-dict.html
欢迎关注我的个人微博:微博上搜索我的名字「张铁蕾」。