看得见的机器学习:零基础看懂神经网络
2020-05-04
关于机器学习,有一个古老的笑话:
Machine learning is like highschool sex. Everyone says they do it, nobody really does, and no one knows what it actually is. [1]
翻译过来意思大概是:
机器学习就像高中生的性爱。每个人都说他们做了,但其实没有人真的做了,也没有人真正知道它到底是什么。
总之,在某种程度上,机器学习确实有很多晦涩难懂的部分。虽然借助TensorFlow、sklearn等工具,机器学习模型以及神经网络通常能被快速地运行起来,但真正弄清背后发生了什么,仍然不是一件容易的事。在本篇文章中,我会试图用直观的方式来解释神经网络。俗话说,「耳听为虚,眼见为实」,本文的目标就是,利用「可视化」的方法,让你亲眼「看到」神经网络在运行时到底做了什么。
本文不会出现一个公式,希望非技术人员也能看懂。希望如此^-^
最简单的神经网络
当今在图像识别或NLP中使用的深度神经网络,都发展出了非常复杂的网络结构,网络层次多达几十层,模型参数多达数十万、上百万个。这样的神经网络理解起来,难度极大,而且计算起来也需要很强的算力。
因此,我们由简入繁,先从最简单的情况入手。
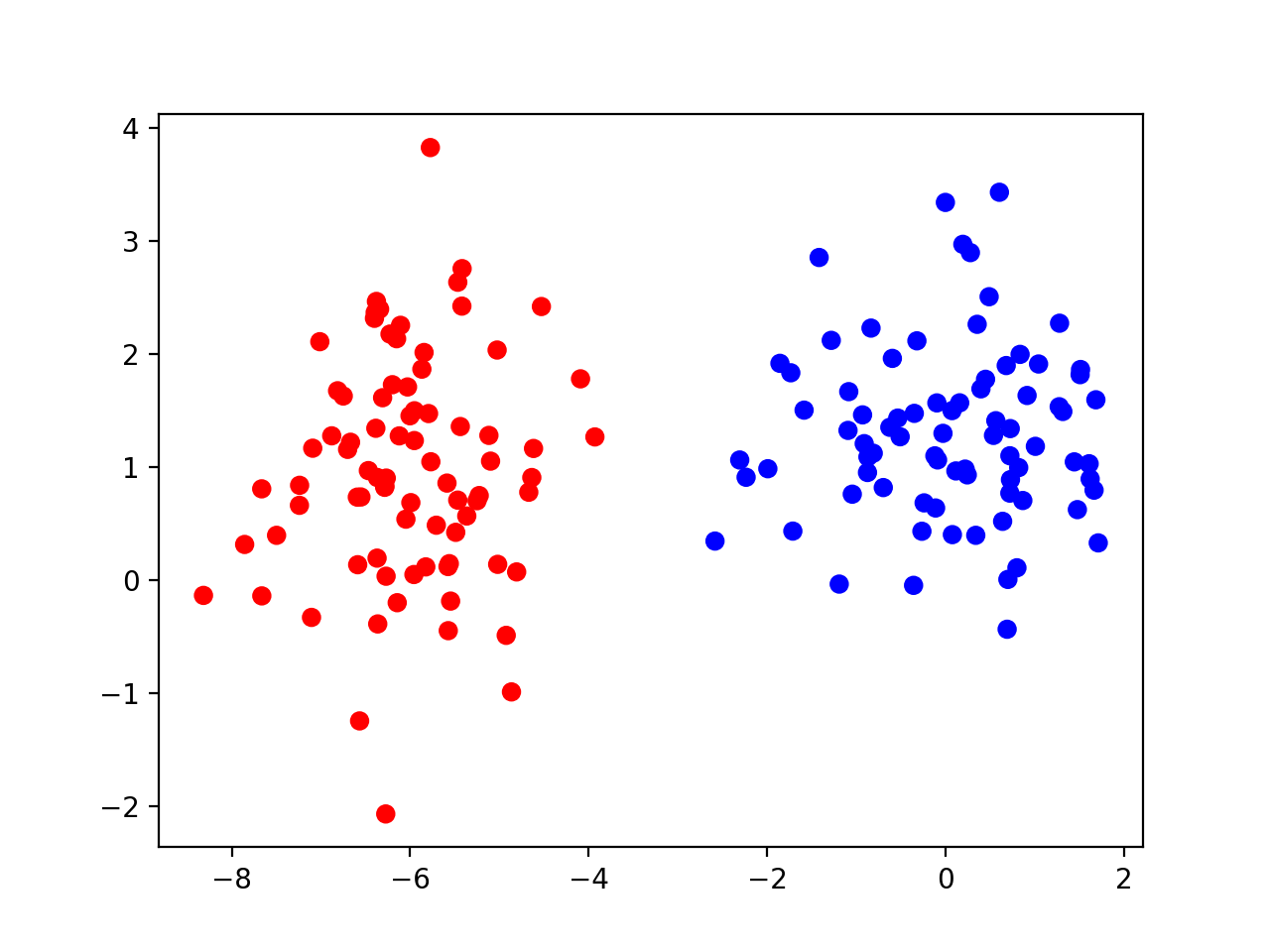
首先,我们考虑一个简单的「二分类」问题。下面展示了一个随机生成的数据集:
上图展示的是总共160个点(包括红色和蓝色),每个点代表一个数据样本。显然,每个样本包含2个特征,这样每个样本才能够在一个二维坐标系中用一个点来表示。红色的点表示该样本属于第1个分类,而蓝色的点表示该样本属于第2个分类。
二分类问题可以理解成:训练出一个分类模型,把上图中160个样本组成的训练集按所属分类分成两份。注意:这个表述并不是很严谨。上图中的样本只是用于训练,而训练出来的模型应该能对「不属于」这个训练集的其它样本进行分类(不过我们现在不关注这一点,可以先忽略掉这个表述上的细节)。
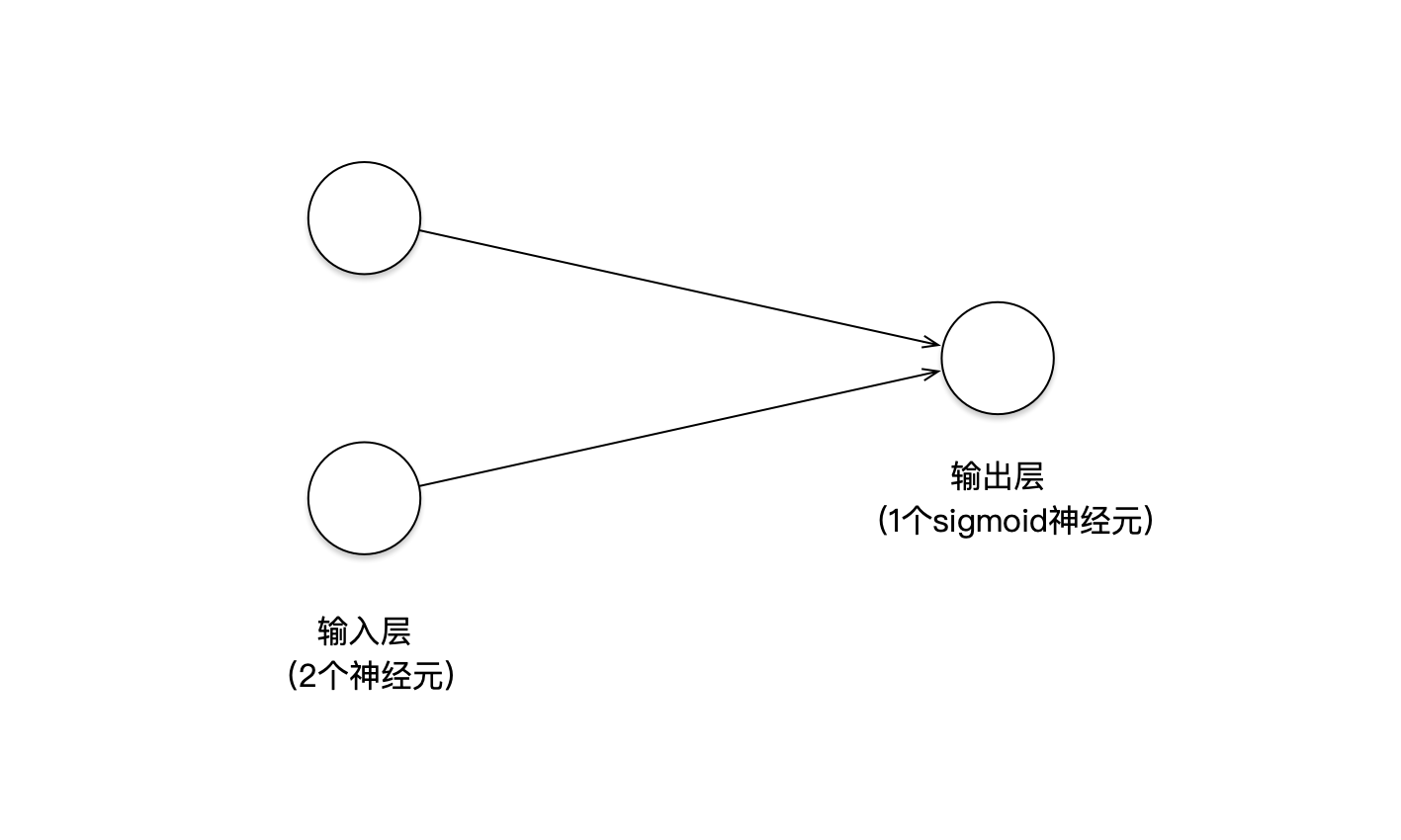
为了完成这个二分类任务,我们有很多种机器学习模型可供选择。但现在我们的目的是为了研究神经网络,所以我们可以设计一个最简单的神经网络,来解决这个分类问题。如下图:
这个神经网络几乎没法再简单了,只有1个输入层和1个输出层,总共只有3个神经元。
经过简单的数学分析就容易看出,这个只有2层的神经网络模型,其实等同于传统机器学习的LR模型(逻辑回归)。也就是说,这是个线性分类器,对它的训练相当于在前面那个二维坐标平面中寻找一条直线,将红色点和蓝色点分开。
根据红色点和蓝色点的位置分布,我们很容易看出,这样的一条直线,很容易找出来(或学习出来)。实际上,上图中这个简单的神经网络,经过训练很容易就能达到100%的分类准确率(accuracy)。
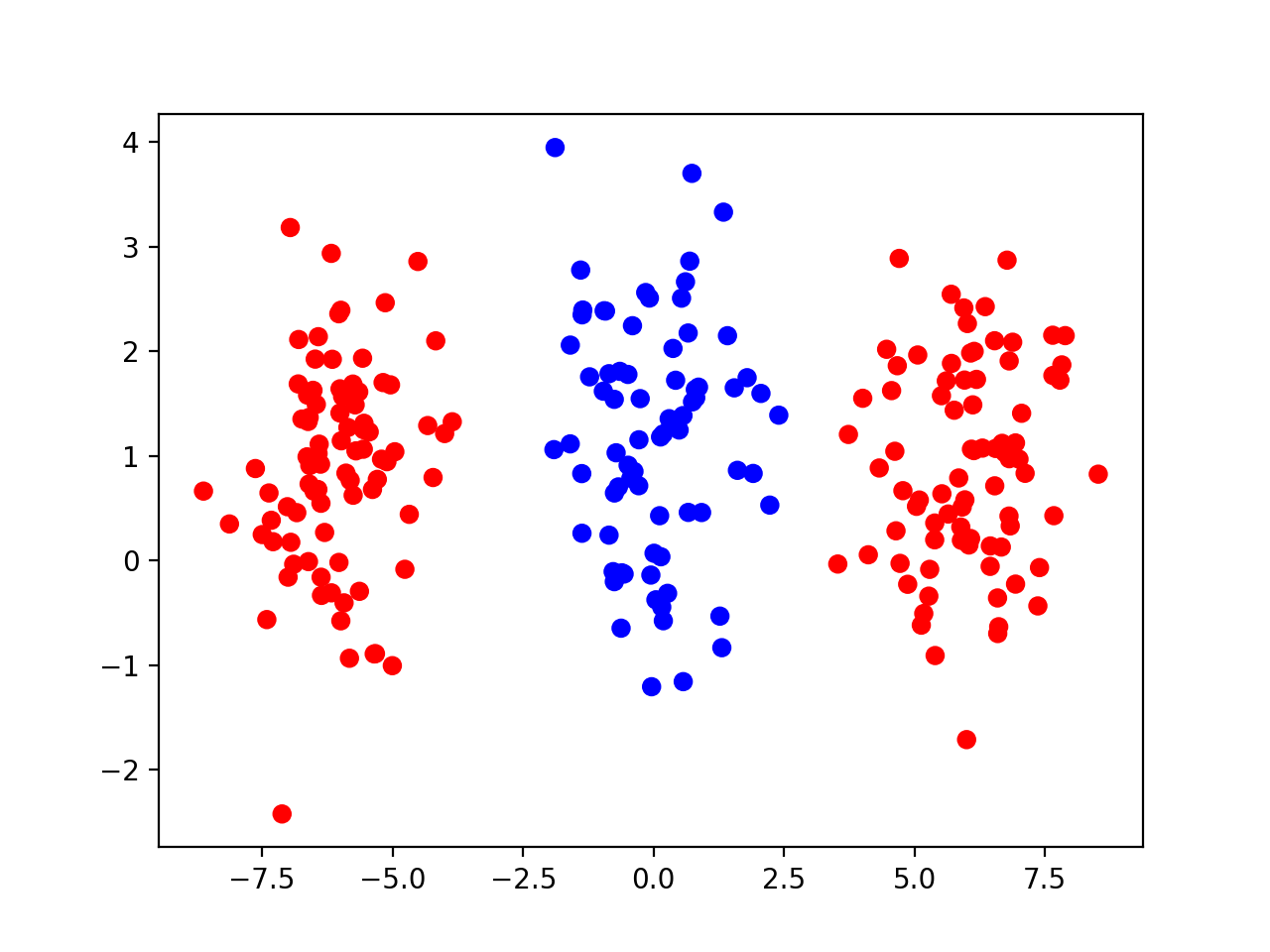
现在,假设我们的数据集变成了下面的样子(红色点分成了两簇,分列蓝色点左右):
如果我们还是使用前面的2层的神经网络,试图画一条直线来把红色点和蓝色点分开,显然就做不到了。我们说,现在这个分成三簇的数据集已经不是「线性可分」的了。实际上,针对最新的这个数据集,前面这个只有2层的神经网络,不管你怎么训练,都只能达到60%~70%左右的分类准确率。
为了提高分类的准确率,比较直观的想法也许是画一条曲线,这样才能把红色点和蓝色点彻底分开。这相当于要对原始输入数据做非线性变换。在神经网络中,我们可以通过增加一个隐藏层(hidden layer)来完成这种非线性变换。修改后的神经网络如下图:
我们看到,修改后的神经网络增加了一层包含2个sigmoid神经元的隐藏层;而输入层和隐藏层之间是全连接的。实际上,当我们重新训练这个带隐藏层的神经网络时,会发现分类的准确率又提升到了100%(或者非常接近100%)。这是为什么呢?
我们可以这样来看待神经网络的计算:每经过一层网络,相当于将样本空间(当然也包括其中的每个样本数据)进行了一次变换。也就是说,输入的样本数据,经过中间的隐藏层时,做了一次变换。而且,由于隐藏层的激活函数使用的是sigmoid,所以这个变换是一个非线性变换。
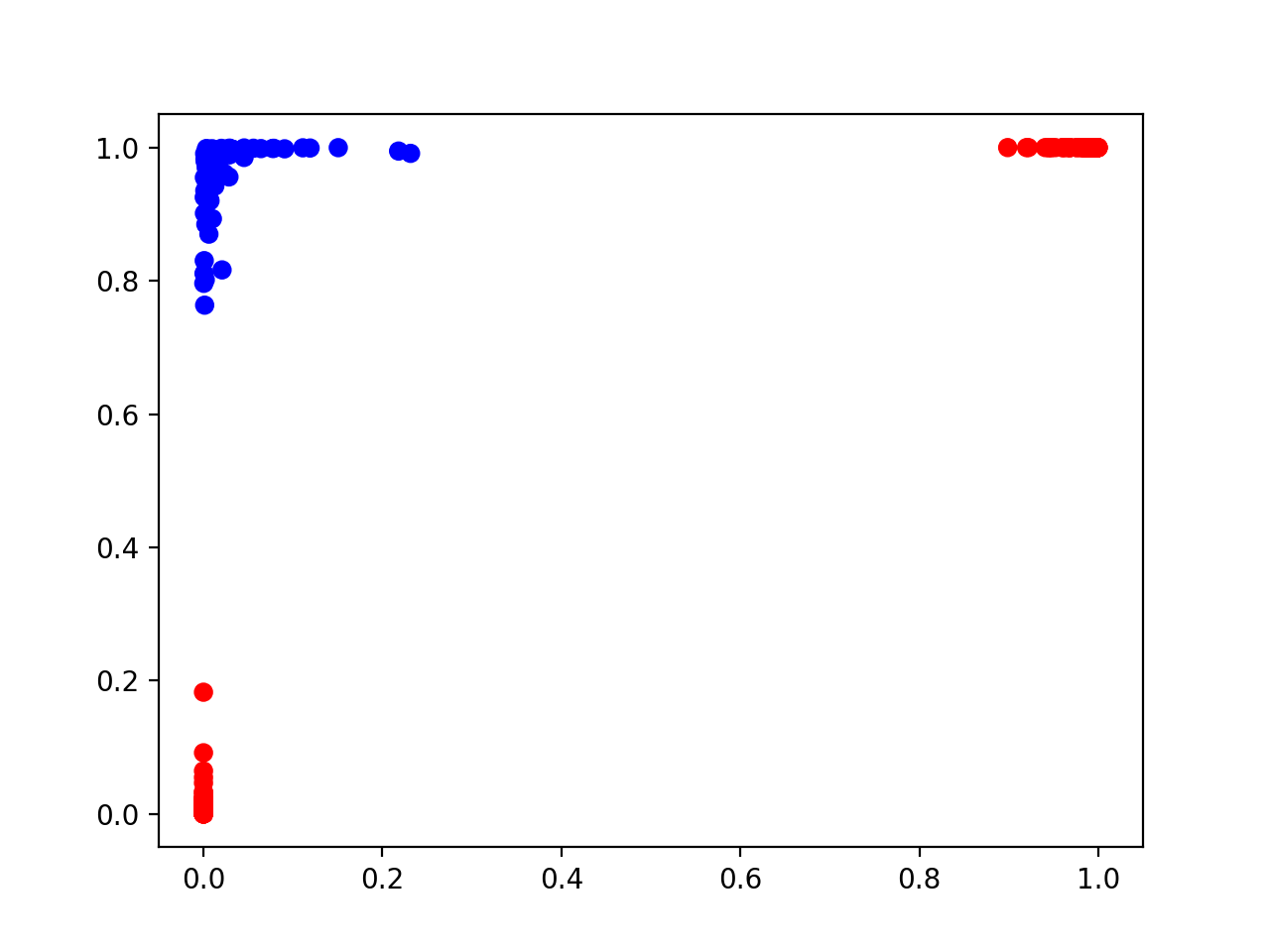
那么,很自然的一个问题是,经过了隐藏层的这一次非线性变换,输入样本变成什么样了呢?下面,我们把隐藏层的2个神经元的输出画到了下图中:
我们发现了一个有趣的现象:变换后的样本数据点,还是分成了三簇,但红色点再也不是分列蓝色点的两侧了。两簇红色点被分别逼到了一个角落里,而蓝色点被逼到了另外一个不同的角落里。很容易看出,现在这个图变成「线性可分」的了。而隐藏层的输出数据,再经过神经网络最后一个输出层的处理,刚好相当于经过了一个线性分类器,很容易用一条直线把红色点和蓝色点分开了。
从隐藏层的输出图像,我们还能发现一些细节:
- 所有的数据坐标(不管是X轴还是Y轴),都落在了(0,1)区间内。因为sigmoid激活函数的特性,正是把实数域映射到(0,1)之间。
- 我们发现,所有的数据都落在某个角落里。这不是偶然,还是因为sigmoid激活函数的特性。当充分训练到sigmoid神经元「饱和」时,它一般是会输出接近0或1的值,而极少可能输出一个接近(0,1)中间的值。
总结一下:从前面的分析,我们大概可以看到这样一个变换过程,就是输入样本在原始空间内本来不是「线性可分」的,而经过了隐藏层的变换处理后,变得「线性可分」了;最后再经过输出层的一次线性分类,成功完成了二分类任务。
当然,这个例子非常简单,只是最简单的神经网络结构。但即使是更复杂的神经网络,原理也是类似的,输入样本每经过一层网络的变换处理,都变得比原来更「可分」一些。我们接下来就看一个稍微复杂一点的例子。
手写体数字识别MNIST
现在我们来考虑一下「手写体数字识别」的问题。
在机器学习的学术界,有一个公开的数据集,称为MNIST[2]。使用神经网络对MNIST的数据进行识别,堪称是神经网络和深度学习领域的「Hello World」。
在MNIST的数据集中,共有70000张手写体数字图片。它们类似下面的样子:
每一张图片都是28像素×28像素的黑白图片,其中每个像素用一个介于[0,255]之间的灰度值表示。
MNIST的数字识别问题,就是给你一张这样的28像素×28像素的图片,用程序区分出它具体是0到9哪一个数字。
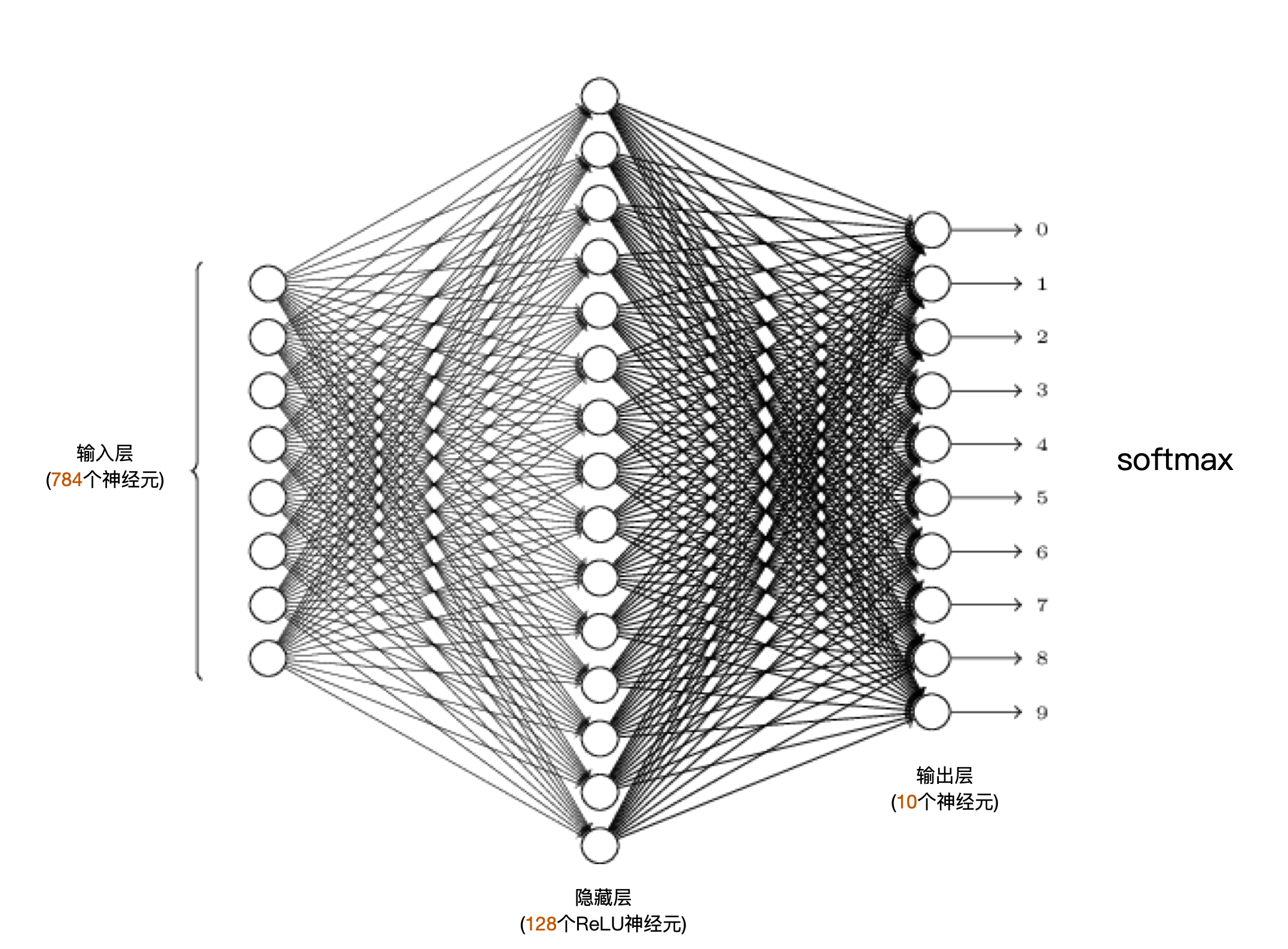
对于这个问题,历史上的最佳成绩是99.79%的识别率,方案使用了卷积神经网络(CNN)。我们这里不想让问题复杂化,因此还是采用普通的全连接的神经网络来求解。我们使用的网络结构如下:
这个神经网络的输入和输出是这样定义的:
- 输入:每次输入一张图片。图片的每个像素的灰度值,除以255后得到一个[0,1]之间的归一化的灰度值,然后输入到输入层的每个神经元上。也就是说,输入层有784个神经元,正好对应一张图片28×28=784个像素。
- 输出:输出层共10个神经元,各个神经元的输出分别对应0到9这几个数字。哪个神经元输出的值最大,我们就可以认为预测结果是对应的那个数字。另外,10个输出值再经过softmax处理,就得到了当前输入图片是各个数字的概率。
对这个神经网络进行训练后,可以很轻松地获得98%左右的正确识别率。那针对这个更宽的神经网络,我们还能使用前面的方法来对它进行可视化的图像绘制吗?
降维
在前面的一小节中,我们的简单神经网络输入层和隐藏层都只有2个神经元,因此可以在一个二维坐标平面中绘制它们的图像。而对于MNIST的这个神经网络,当我们想对它的输入层进行图像绘制的时候,发现它有784维!
如何把784维的特征向量绘制出来?这涉及到对于高维数据可视化的问题。通常来讲,人的大脑只能理解最高3维的空间,对于3维以上的空间,就只能靠抽象思维了。
我们想象一个简单的例子,来感受一下对高维空间进行直观的理解有多么困难:
- 首先,在一个平面内(也就是2维空间),我们可以找到3个两两等距的点,以它们为顶点可以组成一个等边三角形。
- 在一个3维空间内,我们可以找到4个两两等距的点,以它们为顶点可以组成一个正四面体,这个正四面体的每个面都是一个等边三角形。
- 现在,我们上升到4维空间,理论上我们可以找到5个两两等距的点,以它们为顶点可以组成一个我们姑且称之为「正五面体」的东西。继续类比,这个所谓的「正五面体」,它的每个「面」,也就是由5个点中的任意4个点组成的「面」,严格来说不能称它为一个「面」,因为它是一个正四面体。另外需要注意,当我们在这里用「正五面体」这样一个名不副实的名字来命名的时候,还带来了很大的误导性,因为它听起来像是3维空间中的一个「正多面体」。但如果你对数学的历史有所了解的话,那么就应该知道,早在2000多年前,欧几里得就在他的《几何原本》中提出了,3维空间中根本不存在正五面体(实际上3维空间中只有5种正多面体)。
好了,如果你还能跟得上前面最后这一段关于4维空间的描述,那么说明你一定阅读得非常仔细,而且正在一边阅读一边思考^-^但不管怎么说,4维空间的情形已经让人足够恼火了(它们符合逻辑但却不可想象),更别说让我们来想象784维空间中的几何结构了!
因此,我们需要降维(dimensionality reduction)的技术,把高维空间中的数据降低到3维或2维空间内,然后才能可视化地绘制出来,达到一定的「直观理解」的目的。
那降维到底是怎样的一种操作呢?我们仔细回想一下,其实在现实世界中,我们已经碰到过很多降维的情况了。比如下面这张图片:
这是100多年前的一幅名画,名字叫《大碗岛的星期天下午》。在这幅画作中,我们可以感受到海滩远处强烈的纵深感。但任何一幅画作,都是在一张二维的平面上绘制的。所以,画家需要把三体景物投影到二维上,这就是一种「降维」处理。与此类似,我们平常用相机拍出的照片,也是把三维空间「降维」到了二维平面上。这种降维处理普遍存在,可以称为「投影变换」,是线性变换的一种。
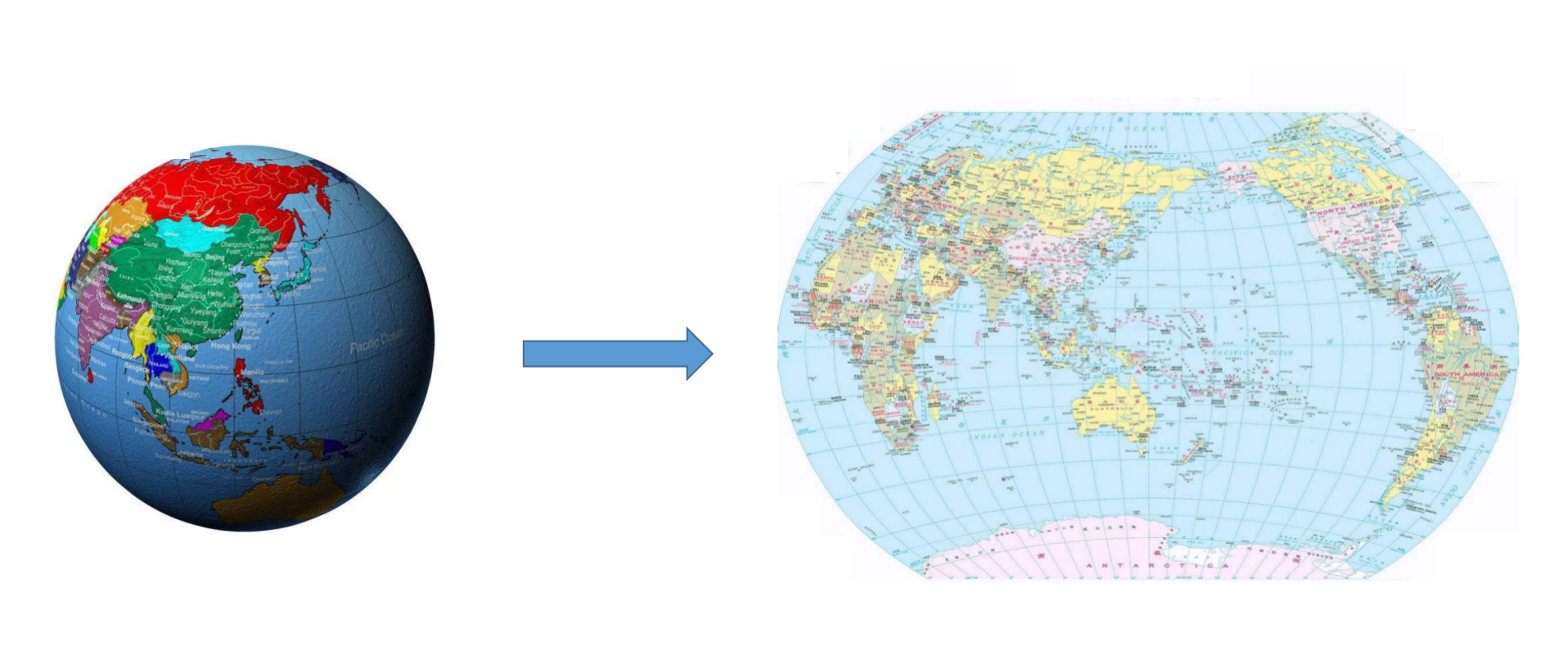
我们再来看一个例子:
图中右侧是一张世界平面地图。本来地球的表面是个三维空间中的球面,但上面的世界地图把整个球面绘制到了一个二维平面上。为了做到这一点,显然地图的绘制者需要把球面摊平,部分区域需要进行一定的拉伸和扭曲。我们把这个绘制过程想象成一个映射:地球表面的一个点,映射到世界平面地图上的一个点上。但所有的点的映射并不满足同样的线性关系,所以这是一个非线性变换。
上面不管是画作、照片的例子,还是世界平面地图的例子,都是把三维降维到二维。但在机器学习中,我们经常需要把从更高维降维到三维或二维。人们发明了各种各样的降维方法,比如PCA (Principal Component Analysis),是一种线性降维方法;MDS (Multi-dimension Scaling)、t-SNE (t-Distributed Stochastic Neighbor Embedding),都是非线性降维方法。
基于k近邻图和力学模型的降维可视化方法
前面提到的各种降维方法,做法不同,也各有侧重点。任何一种解释起来,都要花去很大的篇幅,因此本文不一一详述。考虑到我们接下来的目标,是为了对前一节引入的MNIST神经网络进行直观的可视化展示,所以我们这里采取一种更为直接(也易理解)的方法——一种基于k-NNG (k-Nearest Neighborhood Graph,k近邻图)和力学模型(Force-Directed)的降维可视化方法[3][4]。
这种方法的过程可以如下描述:
- 对于高维空间中的节点计算两两之间的距离,为每个节点找到离它最近的k个节点,分别连接起来建立一条边。这样就创建出了一个由节点和边组成的图数据结构。这个新创建的图有这样的特性:有边直接相连的节点,它们在原高维空间中的位置就是比较接近的;而没有边直接相连的节点,它们在原高维空间中的位置就是比较远的。这个图称为「k近邻图」,也就是k-NNG (k-Nearest Neighborhood Graph)。另外还有一个问题:高维空间中两个节点的距离怎么计算?这其实有很多种计算方法,比较常见的有「欧几里得距离」、「明可夫斯基距离」等。
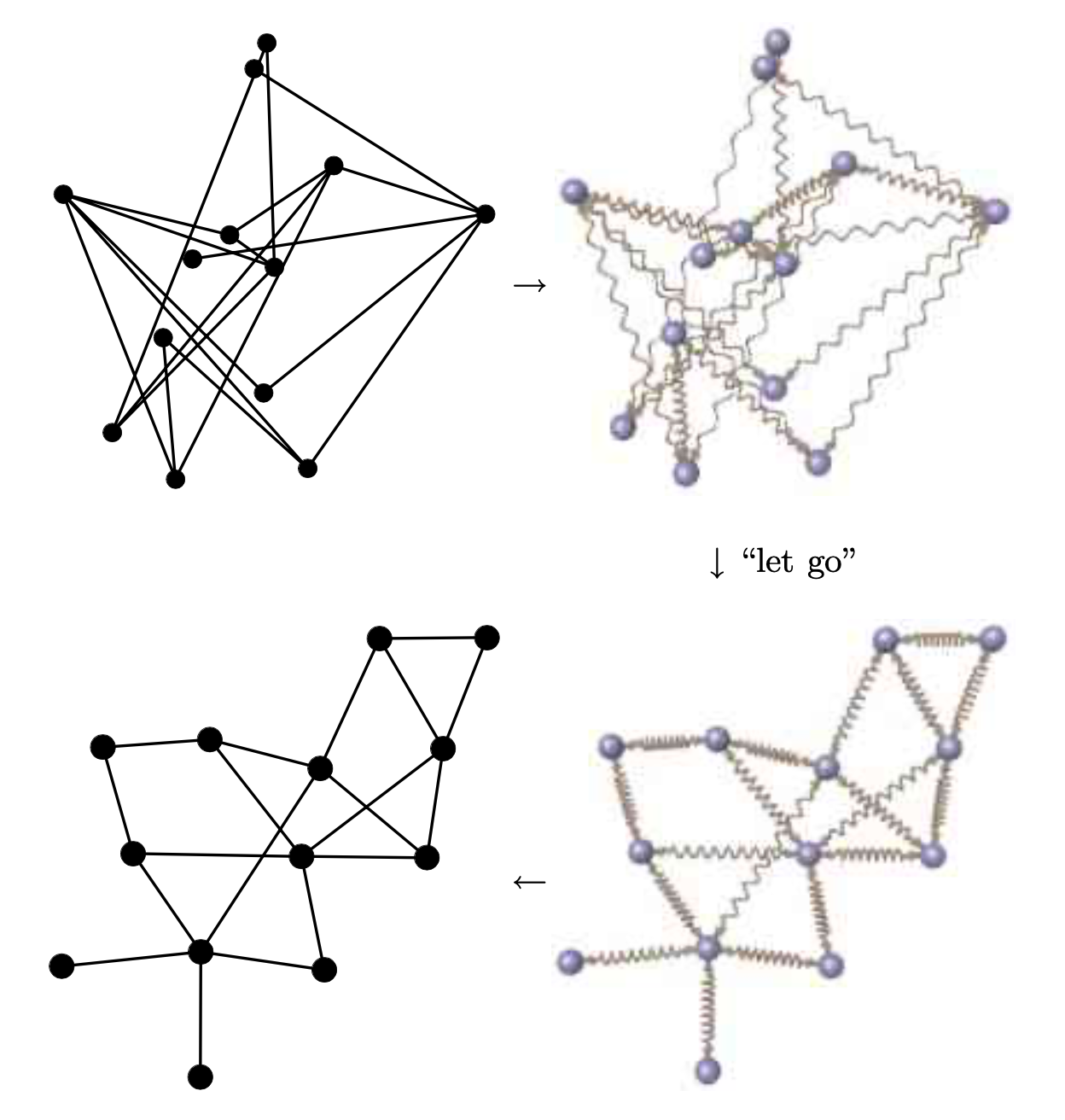
- 将前面一步得到的k近邻图在二维平面中绘制出来。这变成了一个常见的绘图布局的问题,从某种程度上跟电路板的元器件布局有点像。为了让绘制出来的图像清晰易观察,这个绘制过程需要尽量满足一定的条件,比如,边线的交叉应该尽量少;有边相连的节点应该尽可能离得近一些;节点之间不能离得太近(聚在一起),应该尽量均匀地散布在整个坐标系平面上。为了达到这样的要求,我们采用了Fruchterman和Reingold发明的Force-Directed Graph Drawing这种算法。它模拟了物理世界的力学原理,如下图所示:
- 想象左上角的图,把边换成弹簧,把节点换成带电小球;
- 弹簧会倾向于把相邻节点(即有边相连的节点)固定在一个自然长度上(对应原高维空间中的距离),不能太远也不能太近;
- 所有「带电小球」都互相保持斥力,让不相邻的节点互相远离,并促使所有节点尽量散布整个画面;
- 放开手,让各个节点在弹簧和斥力的作用下自由移动,最后达到总体能量最小的状态,这时就得到了左下角那个更好的节点布局。
对于这种方法,我们需要重点关注的是:从高维降到低维,原来高维空间中的哪些几何特性被保持住了?从前面绘制过程的描述容易看出:在原高维空间中距离比较近的节点,在最后绘制的二维图像中,也会在弹簧拉力的作用下离得比较近。只有搞清楚这一点,我们才能通过观看低维的图像,来理解高维的结构。
现在,我们终于做好准备来对MNIST神经网络进行可视化了。
MNIST的可视化
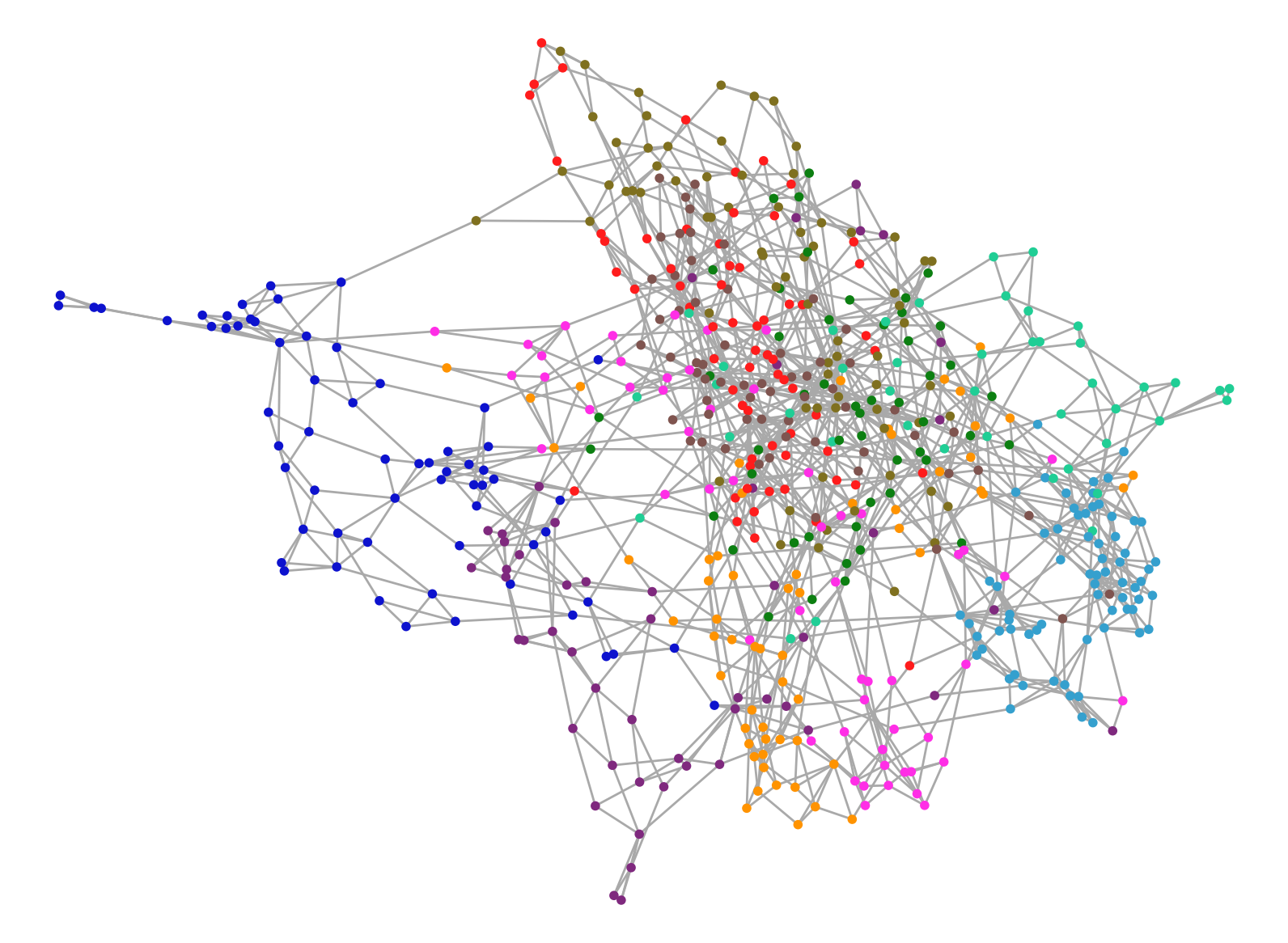
上图是对于MINST神经网络输入层数据的可视化图像(784维)。图中每一个节点都表示一张图片,用一个784维的向量表示;图中每一种颜色表示0到9数字中的一个,相当于节点总共有10种分类。我们可以看出:
- MNIST的原始数据集中,自发展示出了一些结构。表示相同数字的节点,它们在原784维空间中,也会比较接近,因此会自然地聚集成簇。比如,左侧的蓝色节点群,表示数字0;右下角的靛蓝色节点群,表示数字1;而左下角的绛紫色节点群,表示数字6。
- 中间右侧有多种不同类的节点混杂的一起。比如,表示数字9的红色节点,表示数字7的深褐色节点,还有表示数字4的黄绿色节点,相互交织在一起。这表示它们不太容易互相区分开。
上图则是对于MINST神经网络中间隐藏层输出数据的可视化图像(128维)。图中每一个节点还是对应一张图片(即对应原始图片数据经过了隐藏层的变换之后的数据),变成了用一个128维的向量表示;图中每一种颜色仍是表示0到9数字中的一个,还是总共有10种分类。我们可以看出:
- 与前面的MINST原始输入数据相比,节点的混乱程度降低了(我们也可以说,熵值降低了)。这也包括在前面图像中混杂在一起的数字7、数字4和数字9,现在它们都各自聚集成簇了:左侧突出来的深褐色节点群,是数字7;左上角的黄绿色节点群,是数字4;红色节点群,是数字9。这表示更容易把它们相互分开了。
上图是对于MINST神经网络最终的输出层输出数据(经过了softmax处理之后的)的可视化图像(10维)。图中每一个节点还是对应一张图片(即对应原始图片数据经过了整个神经网络的变换之后的数据),变成了一个只有10维的向量;图中每一种颜色仍是表示0到9数字中的一个,还是总共有10种分类。我们可以看出:
- 节点混乱程度极大降低,每类数字都各自聚集在一起。考虑到这张图像里面的节点数量跟前面两张图像里面的节点数量是完全一样的,但散布空间小了很多,说明按照分类的聚集程度达到了很高的程度。实际上,这时候只需要对最后这个10维向量做一个简单的argmax判断,就可以以很高的准确率识别出具体数字了。这表示,最后的输出具有很高的「可分」度。
小结
在本文中,通过对神经网络的可视化研究,我们发现:从原始的特征输入出发,神经网络每经过一层的变换处理,都在抽象程度上离问题的目标更接近一点。拿MNIST的手写体数字识别问题来说,目标是一个多分类问题,即把图片归到0到9这10个类别中的一个。最开始输入的是原始的图片像素数据,每经过一次网络层变换处理之后,数据就变得比原来更「可分」一点,也就是离分类的目标更接近一点。
这是一种典型的对信息进行整合的过程。就像许多现实世界中的情形一样,庞杂的细节,只有经过有效地整合,我们才能获得真正的「感知」或「认知」。
而对于类似图像识别这样的简单的感知行为,人类甚至意识不到这个信息整合过程的存在。把人眼看到物体这个过程拆解开来看,物理世界的光子进入人眼感光细胞,会产生大量的细节数据。而这些数据势必经过了人脑中一个类似神经网络(肯定比神经网络更高级)的结构来处理,将这些细节数据经过整合之后,才让我们在宏观层面认识到眼前看到了什么物体。对人脑来说,这个过程是瞬间发生的,它快速、准确,而且低能耗。如果我们要设计一种能识别物体的模型,最好的方法也许是完全复制人脑的处理机制。但这些机制都是未知,或者至少我们所知非常有限。因此,我们只能近似、参考、模仿人脑的机制。
最后,我们今天所讨论的可视化技术,只是对于机器学习追求可解释性的技术(Interpretability Techniques)中非常初级的一部分。它可能会对我们如何修正现有模型或者如何更好地训练模型,提供参考价值,但是,它很可能无法帮助我们从头发明出一个颠覆式的学习机制。就像我们在上一篇文章《程序员眼中的「技术-艺术」光谱》中所讨论的那样,新模型的设计,或者一种崭新学习机制的发明,仍然是一门需要灵感的「艺术」。
(正文完)
参考文献:
- [1] https://github.com/antirez/neural-redis
- [2] MNIST data set. http://yann.lecun.com/exdb/mnist/
- [3] Computes the (weighted) graph of k-Neighbors. https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.kneighbors_graph.html
- [4] Fruchterman-Reingold force-directed algorithm. https://networkx.github.io/documentation/stable/reference/generated/networkx.drawing.layout.spring_layout.html#networkx.drawing.layout.spring_layout
其它精选文章:
- 给普通人看的机器学习(一):优化理论
- 用统计学的观点看世界:从找不到东西说起
- 漫谈业务与平台
- 漫谈分布式系统、拜占庭将军问题与区块链
- 在技术和业务中保持平衡
- 三个字节的历险
- 做技术的五比一原则
- 知识的三个层次
原创文章,转载请注明出处,并包含下面的二维码!否则拒绝转载!
本文链接:http://zhangtielei.com/posts/blog-nn-visualization.html
欢迎关注我的个人微博:微博上搜索我的名字「张铁蕾」。